
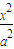 +
+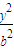 =1(a>b>0)的左焦点为F1(-2,0),左准线l1与x轴交于点N(-3,0),过点N且倾斜角为30°的直线l交椭圆于A、B两点.
=1(a>b>0)的左焦点为F1(-2,0),左准线l1与x轴交于点N(-3,0),过点N且倾斜角为30°的直线l交椭圆于A、B两点.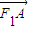 •
•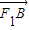 =0,得到F1A⊥F1B,所以点F1在以线段AB为直径的圆上.
=0,得到F1A⊥F1B,所以点F1在以线段AB为直径的圆上.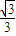 (x+3),
(x+3),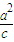 =3,解得a2=6,
=3,解得a2=6,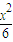 +
+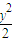 =1.
=1.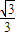 (x+3),②
(x+3),② .
.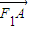 •
•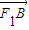 =(x1+2,y1)•(x2+2,y2)=(x1+2)(x2+2)+y1y2
=(x1+2,y1)•(x2+2,y2)=(x1+2)(x2+2)+y1y2 [x1x2+3(x1+x2)+9]=
[x1x2+3(x1+x2)+9]= x1x2+3(x1+x2)+7=0,
x1x2+3(x1+x2)+7=0,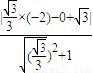 =
= 为所求.
为所求.

科目:高中数学 来源:2007年天津市高考数学试卷(理科)(解析版) 题型:解答题
 =1(a>b>0)的左、右焦点分别为F1,F2,A是椭圆上的一点,AF2⊥F1F2,原点O到直线AF1的距离为
=1(a>b>0)的左、右焦点分别为F1,F2,A是椭圆上的一点,AF2⊥F1F2,原点O到直线AF1的距离为 .
. ;
;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 +
+ =1(a>b>0)的离心率为e,A为椭圆上一点,弦AB,AC分别过焦点F1,F2.
=1(a>b>0)的离心率为e,A为椭圆上一点,弦AB,AC分别过焦点F1,F2. =λ1
=λ1 ,
,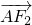 =λ2
=λ2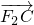 ,当A在椭圆上运动时,求证:λ1+λ2为定值.
,当A在椭圆上运动时,求证:λ1+λ2为定值.查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西省九江市都昌二中高三(上)周考数学试卷(6)(文科)(解析版) 题型:解答题
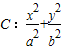 =1(a>b>0)过点
=1(a>b>0)过点 ,且左焦点为
,且左焦点为
 •
•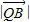 =
=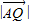 •
• ,证明:点Q总在某定直线上.
,证明:点Q总在某定直线上.查看答案和解析>>
科目:高中数学 来源:2012-2013学年黑龙江省哈尔滨九中高二(上)期末数学试卷(文科)(解析版) 题型:解答题
 =1(a>b>0)过点
=1(a>b>0)过点 ,且左焦点为
,且左焦点为
 •
• =
= •
• ,证明:点Q总在某定直线上.
,证明:点Q总在某定直线上.查看答案和解析>>
科目:高中数学 来源:2009年高考数学压轴试卷集锦(8)(解析版) 题型:解答题
 =1(a>b>0)的焦距为2c.以点O为圆心,a为半径作圆M.若过点P(
=1(a>b>0)的焦距为2c.以点O为圆心,a为半径作圆M.若过点P( ,0)所作圆M的两条切线互相垂直,则该椭圆的离心率为______
,0)所作圆M的两条切线互相垂直,则该椭圆的离心率为______查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com