练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，长方形中，，点分别在线段（含端点）上，为中点，，设.

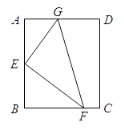
    （1）求角的取值范围；

    （2）求出周长关于角的函数解析式，并求周长的取值范围.

    【答案】（1）（2），，周长的取值范围为

    【解析】

    （1）结合图像可得当点位于点时，角取最大值，点位于点时，取最大值，角取最小值，在直角三角形中求解即可.

    （2）在中，求出，在中，求得，在中，根据勾股定理得，从而可得，通分可得，令，借助三角函数的性质即可求解.

    （1）由题意知，当点位于点时，角取最大值，

    此时，因为，所以

    当点位于点时，取最大值，角取最小值，

    此时，所以

    故所求的取值集合为

    （2）在中，，，所以

    在中，，，所以

    在中，有勾股定理得

    因为，所以，

    所以

    所以，

    令，则

    所以

    因为，，

    所以

    所以

    所以周长的取值范围为

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某医院一天派出医生下乡医疗，派出医生人数及其概率如下：

    医生人数

    0

    1

    2

    3

    4

    5人及以上

    概率

    0.1

    0.16

    0.3

    0.2

    0.2

    0.04

    求：(1)派出医生至多2人的概率；

    (2)派出医生至少2人的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某学校科技节需要同学设计一幅矩形纸板宣传画，要求画面的面积为（如图中的阴影部分），画面的上、下各留空白，左、右各留空白.

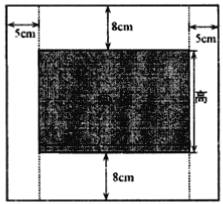
    （1）如何设计画面的高与宽的尺寸，才能使整个宣传画所用纸张面积最小？

    （2）如果按照第一问这样制作整个宣传画，在科技节结束以后，这整个宣传画纸板可再次作为某实验道具，并要求从整个宣传画板的四个角各截取一个相同的小正方形，做成一个长方体形的无盖容器.问截下的小正方形的边长（也就是该容器的高）是多少时，该容器的容积最大？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数.

    (1) 解不等式；

    (2) 设函数，若函数为偶函数，求实数的值；

    (3) 当时，是否存在实数（其中），使得不等式恒成立？若存在，求出的取值范围；若不存在，说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2015年我国将加快阶梯水价推行，原则是“保基本、建机制、促节约”，其中“保基本”是指保证至少80%的居民用户用水价格不变．为响应国家政策，制定合理的阶梯用水价格，某城市采用简单随机抽样的方法分别从郊区和城区抽取5户和20户居民的年人均用水量进行调研，抽取的数据的茎叶图如下（单位：吨）：

    （1）在郊区的这5户居民中随机抽取2户，求其年人均用水量都不超过30吨的概率；

    （2）设该城市郊区和城区的居民户数比为，现将年人均用水量不超过30吨的用户定义为第一阶梯用户，并保证这一梯次的居民用户用水价格保持不变．试根据样本估计总体的思想，分析此方案是否符合国家“保基本”政策．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知斜三棱柱， ， ， 在底面上的射影恰为的中点，且.

    （1）求证： 平面；

    （2）求到平面的距离；

    （3）求二面角的平面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）求函数的最大值；

    （2）设,证明.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知集合M=，对它的非空子集A，可将A中每个元素K都乘以再求和（如A=，可求得和为），则对M的所有非空子集，这些和的总和是__________________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图,在三棱柱中,侧棱底面,为棱的中点.,,.

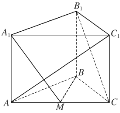
    （1）求证：平面；

    （2）在棱上是否存在点,使得平面平面？如果存在,求此时的值；如果不存在,请说明理由.

    查看答案和解析>>

    同步练习册答案