
【题目】已知圆![]() 关于直线
关于直线![]() 对称的圆为
对称的圆为![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)过点![]() 作直线
作直线![]() 与圆
与圆![]() 交于
交于![]() 两点,
两点, ![]() 是坐标原点,是否存在这样的直线
是坐标原点,是否存在这样的直线![]() ,使得在平行四边形
,使得在平行四边形![]() 中
中![]() ?若存在,求出所有满足条件的直线
?若存在,求出所有满足条件的直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
【答案】(1)![]() (2)存在直线
(2)存在直线![]() 和
和![]()
【解析】试题分析:(1)将圆的一般方程转化为标准方程,将圆关于直线对称问题转化为点关于直线对称问题,进而求出圆的方程;(2)先由条件判定四边形![]() 为矩形,将问题转化为判定两直线垂直,利用平面向量是数量积为0进行求解.
为矩形,将问题转化为判定两直线垂直,利用平面向量是数量积为0进行求解.
试题解析:(1)圆![]() 化为标准为
化为标准为![]() ,
,
设圆![]() 的圆心
的圆心![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,则
,则![]() ,
,
且![]() 的中点
的中点![]() 在直线
在直线![]() 上,
上,
所以有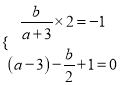 ,
,
解得: ![]() ,
,
所以圆![]() 的方程为
的方程为![]() .
.
(2)由![]() ,所以四边形
,所以四边形![]() 为矩形,所以
为矩形,所以![]() .
.
要使![]() ,必须使
,必须使![]() ,即:
,即: ![]() .
.
①当直线![]() 的斜率不存在时,可得直线
的斜率不存在时,可得直线![]() 的方程为
的方程为![]() ,与圆
,与圆![]()
交于两点![]() ,
, ![]() .
.
因为![]() ,所以
,所以![]() ,所以当直线
,所以当直线![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 满足条件.
满足条件.
②当直线![]() 的斜率存在时,可设直线
的斜率存在时,可设直线![]() 的方程为
的方程为![]() .
.
设![]()
由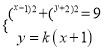 得:
得: ![]() .由于点
.由于点![]() 在圆
在圆![]() 内部,所以
内部,所以![]() 恒成立,
恒成立,
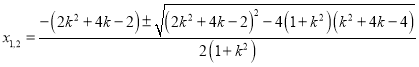 ,
,
![]() ,
, ![]() ,
,
要使![]() ,必须使
,必须使![]() ,即
,即![]() ,
,
也就是: ![]()
整理得: ![]()
解得: ![]() ,所以直线
,所以直线![]() 的方程为
的方程为![]()
存在直线![]() 和
和![]() ,它们与圆
,它们与圆![]() 交
交![]() 两点,且四边形
两点,且四边形![]() 对角线相等.
对角线相等.


 天天向上口算本系列答案
天天向上口算本系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() 为自然对数的底数.
为自然对数的底数.
(Ⅰ)求曲线![]() 在
在![]() 处的切线方程;
处的切线方程;
(Ⅱ)关于![]() 的不等式
的不等式![]() 在
在![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)关于![]() 的方程
的方程![]() 有两个实根
有两个实根![]() ,
, ![]() ,求证:
,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】黄种人群中各种血型的人所占的比例如下:
血型 | A | B | AB | O |
该血型的人所占比例(%) | 28 | 29 | 8 | 35 |
已知同种血型的人可以输血,O型血可以输给任何一种血型的人,其他不同血型的人不能互相输血,小明是B型血,若小明因病需要输血,问:
(1)任找一个人,其血可以输给小明的概率是多少?
(2)任找一个人,其血不能输给小明的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间共有![]() 名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.
名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.
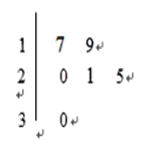
(Ⅰ) 根据茎叶图计算样本均值;
(Ⅱ) 日加工零件个数大于样本均值的工人为优秀工人,根据茎叶图推断该车间![]() 名工人中有几名优秀工人;
名工人中有几名优秀工人;
(Ⅲ) 从该车间![]() 名工人中,任取2人,求恰有1名优秀工人的概率.
名工人中,任取2人,求恰有1名优秀工人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某观测站在港口A的南偏西40°方向的C处,测得一船在距观测站31海里的B处,正沿着从港口出发的一条南偏东20°的航线上向港口A开去,当船走了20海里到达D处,此时观测站又测得CD等于21海里,问此时船离港口A处还有多远? 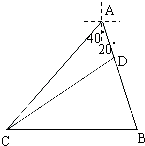
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 且
且![]() 为常数).
为常数).
(1)当![]() 时,讨论函数
时,讨论函数![]() 在
在![]() 的单调性;
的单调性;
(2)设![]() 可求导数,且它的导函数
可求导数,且它的导函数![]() 仍可求导数,则
仍可求导数,则![]() 再次求导所得函数称为原函数
再次求导所得函数称为原函数![]() 的二阶函数,记为
的二阶函数,记为![]() ,利用二阶导函数可以判断一个函数的凹凸性.一个二阶可导的函数在区间
,利用二阶导函数可以判断一个函数的凹凸性.一个二阶可导的函数在区间![]() 上是凸函数的充要条件是这个函数在
上是凸函数的充要条件是这个函数在![]() 的二阶导函数非负.
的二阶导函数非负.
若![]() 在
在![]() 不是凸函数,求
不是凸函数,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且![]()
(1)求证:不论![]() 为何值,总有平面BEF⊥平面ABC;
为何值,总有平面BEF⊥平面ABC;
(2)当λ为何值时,平面BEF⊥平面ACD ?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2.∠ABC=∠DBC=120°,E、F分别为AC、DC的中点. 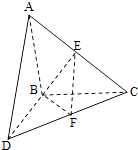
(1)求证:EF⊥BC;
(2)求二面角E﹣BF﹣C的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com