
已知函数![]() ,且
,且![]()
(1) 试用含![]() 的代数式表示b,并求
的代数式表示b,并求![]() 的单调区间;
的单调区间;
(2)令![]() ,设函数
,设函数![]() 在
在![]() 处取得极值,记点M (
处取得极值,记点M (![]() ,
,![]() ),N(
),N(![]() ,
,![]() ),P(
),P(![]() ),
), ![]() ,请仔细观察曲线
,请仔细观察曲线![]() 在点P处的切线与线段MP的位置变化趋势,并解释以下问题:
在点P处的切线与线段MP的位置变化趋势,并解释以下问题:
(I)若对任意的m ![]() (
(![]() , x
, x![]() ),线段MP与曲线f(x)均有异于M,P的公共点,试确定t的最小值,并证明你的结论;
),线段MP与曲线f(x)均有异于M,P的公共点,试确定t的最小值,并证明你的结论;
(II)若存在点Q(n ,f(n)), x ![]() n< m,使得线段PQ与曲线f(x)有异于P、Q的公共点,请直接写出m的取值范围(不必给出求解过程)
n< m,使得线段PQ与曲线f(x)有异于P、Q的公共点,请直接写出m的取值范围(不必给出求解过程)
略
解法1
(Ⅰ)依题意,得![]()
由![]() .
.
从而![]()
令![]()
①当a>1时, ![]()
当x变化时,![]() 与
与![]() 的变化情况如下表:
的变化情况如下表:
| x |
|
|
|
|
| + | - | + |
|
| 单调递增 | 单调递减 | 单调递增 |
由此得,函数![]() 的单调增区间为
的单调增区间为![]() 和
和![]() ,单调减区间为
,单调减区间为![]() 。
。
②当![]() 时,
时,![]() 此时有
此时有![]() 恒成立,且仅在
恒成立,且仅在![]() 处
处![]() ,故函数
,故函数![]() 的单调增区间为R
的单调增区间为R
③当![]() 时,
时,![]() 同理可得,函数
同理可得,函数![]() 的单调增区间为
的单调增区间为![]() 和
和![]() ,单调减区间为
,单调减区间为![]()
综上:
当![]() 时,函数
时,函数![]() 的单调增区间为
的单调增区间为![]() 和
和![]() ,单调减区间为
,单调减区间为![]() ;
;
当![]() 时,函数
时,函数![]() 的单调增区间为R;
的单调增区间为R;
当![]() 时,函数
时,函数![]() 的单调增区间为
的单调增区间为![]() 和
和![]() ,单调减区间为
,单调减区间为![]() .
.
(Ⅱ)由![]() 得
得![]() 令
令![]() 得
得![]()
由(1)得![]() 增区间为
增区间为![]() 和
和![]() ,单调减区间为
,单调减区间为![]() ,所以函数
,所以函数![]() 在处
在处![]() 取得极值,故M(
取得极值,故M(![]() )N(
)N(![]() )。
)。
观察![]() 的图象,有如下现象:
的图象,有如下现象:
①当m从-1(不含-1)变化到3时,线段MP的斜率与曲线![]() 在点P处切线的斜率
在点P处切线的斜率![]() 之差Kmp-
之差Kmp-![]() 的值由正连续变为负。
的值由正连续变为负。
②线段MP与曲线是否有异于H,P的公共点与Kmp-![]() 的m正负有着密切的关联;
的m正负有着密切的关联;
③Kmp-![]() =0对应的位置可能是临界点,故推测:满足Kmp-
=0对应的位置可能是临界点,故推测:满足Kmp-![]() 的m就是所求的t最小值,下面给出证明并确定的t最小值.曲线
的m就是所求的t最小值,下面给出证明并确定的t最小值.曲线![]() 在点
在点![]() 处的切线斜率
处的切线斜率![]() ;
;
线段MP的斜率Kmp![]()
当Kmp-![]() =0时,解得
=0时,解得![]()
直线MP的方程为![]()
令![]()
当![]() 时,
时,![]() 在
在![]() 上只有一个零点
上只有一个零点![]() ,可判断
,可判断![]() 函数在
函数在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,又
上单调递减,又![]() ,所以
,所以![]() 在
在![]() 上没有零点,即线段MP与曲线
上没有零点,即线段MP与曲线![]() 没有异于M,P的公共点。
没有异于M,P的公共点。
当![]() 时,
时,![]() .
.![]()
所以存在![]() 使得
使得![]()
即当![]() MP与曲线
MP与曲线![]() 有异于M,P的公共点
有异于M,P的公共点
综上,t的最小值为2.
(2)类似(1)于中的观察,可得m的取值范围为![]()
解法2:
(1)同解法一.
(2)由![]() 得
得![]() ,令
,令![]() ,得
,得![]()
由(1)得的![]() 单调增区间为
单调增区间为![]() 和
和![]() ,单调减区间为
,单调减区间为![]() ,所以函数在处取得极值。故M(
,所以函数在处取得极值。故M(![]() ).N(
).N(![]() )
)
(Ⅰ) 直线MP的方程为![]()
由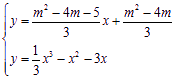
得![]()
线段MP与曲线![]() 有异于M,P的公共点等价于上述方程在(-1,m)上有根,即函数
有异于M,P的公共点等价于上述方程在(-1,m)上有根,即函数
![]() 上有零点.
上有零点.
因为函数![]() 为三次函数,所以
为三次函数,所以![]() 至多有三个零点,两个极值点.
至多有三个零点,两个极值点.
又![]() .因此,
.因此, ![]() 在
在![]() 上有零点等价于
上有零点等价于![]() 在
在![]() 内恰有一个极大值点和一个极小值点,即
内恰有一个极大值点和一个极小值点,即![]() 内有两不相等的实数根.
内有两不相等的实数根.
等价于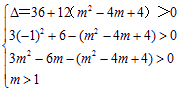 即
即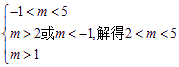
又因为![]() ,所以m 的取值范围为(2,3),从而满足题设条件的r的最小值为2.
,所以m 的取值范围为(2,3),从而满足题设条件的r的最小值为2.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源:2014届江苏省高一上学期第二次月考数学试卷 题型:解答题
(本小题满分14分)已知函数 ,且
,且 .
.
(1)判断 的奇偶性并说明理由;
的奇偶性并说明理由;
(2)判断 在区间
在区间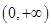 上的单调性,并证明你的结论;
上的单调性,并证明你的结论;
(3)若在区间 上,不等式
上,不等式 恒成立,试确定实数
恒成立,试确定实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2010-2011年浙江省高二下学期期中考试数学理卷 题型:解答题
已知函数 ,且
,且
(1)求函数 的表达式;
的表达式;
(2)若数列 的项满足
的项满足 ,试求
,试求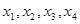 ;
;
(3)猜想数列 的通项,并用数学归纳法证明.
的通项,并用数学归纳法证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com