
分析 写出①的否命题并举反例判断①;由a>1时,不等式ax2-2ax+a+3>0对应的二次方程的判别式小于0判断②;直接写出原命题的逆命题判断③;写出原命题的逆否命题判断④.
解答 解:①“若a2<b2,则a<b”的否命题为:“若a2≥b2,则a≥b”,为假命题,如(-3)2≥(-2)2,但-3<-2,故①是假命题;
②a>1时,不等式ax2-2ax+a+3>0对应的二次方程的判别式=(-2a)2-4a2-12a=-12a<0,可得“若a>1,则ax2-2ax+a+3>0的解集为R”为真命题,则其逆否命题为真命题,故②是真命题;
③“全等三角形面积相等”的逆命题是:“面积相等的三角形全等”,是假命题,故③是假命题;
④“若$\sqrt{3}$x(x≠0)为有理数,则x为无理数”的逆否命题是:“若x为有理数,则$\sqrt{3}$x(x≠0)为无理数”,是真命题,故④是真命题.
故答案为:②④.
点评 本题考查命题的真假判断与应用,考查了命题的逆命题、否命题和逆否命题,是中档题.


科目:高中数学 来源: 题型:选择题
 一个几何体的三视图如图所示,则该几何体的体积等于( )
一个几何体的三视图如图所示,则该几何体的体积等于( )| A. | 8+4π | B. | 8+2π | C. | 8+$\frac{4}{3}$π | D. | 8+$\frac{2}{3}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某学校一个生物兴趣小组对学校的人工湖中养殖的某种鱼类进行观测研究,在饲料充足的前提下,兴趣小组对饲养时间x(单位:月)与这种鱼类的平均体重y(单位:千克)得到一组观测值,如下表:
某学校一个生物兴趣小组对学校的人工湖中养殖的某种鱼类进行观测研究,在饲料充足的前提下,兴趣小组对饲养时间x(单位:月)与这种鱼类的平均体重y(单位:千克)得到一组观测值,如下表:| xi(月) | 1 | 2 | 3 | 4 | 5 |
| yi(千克) | 0.5 | 0.9 | 1.7 | 2.1 | 2.8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
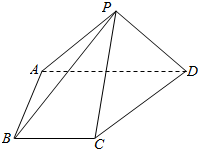 如图,四棱锥P-ABCD中,平面PAD⊥底面ABCD,PA⊥PD,PA=PD,BC∥AD,AB⊥AD,AD=2AB=2BC=2.
如图,四棱锥P-ABCD中,平面PAD⊥底面ABCD,PA⊥PD,PA=PD,BC∥AD,AB⊥AD,AD=2AB=2BC=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{\sqrt{3}}{5}$ | B. | $\frac{\sqrt{3}}{5}$ | C. | -$\frac{3}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,AB是半圆O的直径,且AB=8,点C为半圆上的一点.将此半圆沿BC所在的直线折叠,若圆弧BC恰好过圆心O,则图中阴影部分的面积是$\frac{8π}{3}$.(结果保留π)
如图,AB是半圆O的直径,且AB=8,点C为半圆上的一点.将此半圆沿BC所在的直线折叠,若圆弧BC恰好过圆心O,则图中阴影部分的面积是$\frac{8π}{3}$.(结果保留π)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com