Question

首先指出下列函数是怎样复合的，然后求导.

(1)y=(2x-1)⁵；

(2)y=;

(3)y=;

Answer 1

分析：先设中间变量，把复合函数的分解过程弄清楚，然后再用复合函数的求导法则求得导数.

解：(1)设μ=2x-1,则y=μ⁵,

∴y_x′=y_μ′·μ_x′=5μ⁴·(2x-1)′

=5(2x-1)⁴·2

=10(2x-1)⁴.

(2)设μ=ax²+bx+c则y=μ,

∴y_x′=y_μ′·μ_x′=(ax²+bc+c)(2ax+b)=.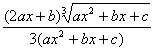

(3)方法一：μ=1-2x,y=μ^-5

y_x′=y_μ′·μ_x′=-5μ^-6·(-2)

=10(1-2x)^-6.

方法二：∵y==()⁵,

令y=μ⁵,μ=,v=1-2x

y_x′=y_μ′·μ_v′·v_x′=5μ⁴·(-v^-2)·(-2)

=10()⁴·v^-2=10v^-6=10(1-2x)^-6.