
(满分12分)分已知函数 .
.
(1)求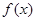 的最小正周期及
的最小正周期及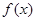 的最小值;
的最小值;
(2)若 ,且
,且 ,求
,求 的值.
的值.
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源:2011届广东省高州市南塘中学高三上学期16周抽考数学理卷 题型:解答题
(本小题满分12分)
对于函数f(x),若存在x0∈R,使f(x0)=x0成立,则称x0为f(x)的不动点。如果函数 有且只有两个不动点0,2,且
有且只有两个不动点0,2,且
(1)求函数f(x)的解析式;
(2)已知各项不为零的数列 (
( 为
为 数列前n项和),求数列通项
数列前n项和),求数列通项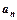 ;
;
(3)如果数列 满足
满足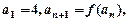 ,求证:当
,求证:当 时,恒有
时,恒有 成立.
成立.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江西省高三五月模拟考试(一)理科数学试卷(解析版) 题型:解答题
(本小题满分12分)某工厂生产甲、乙两种产品,每种产品都是经过第一道和第二道工序加工而成,两道工序的加工结果相互独立,每道工序的加工结果均有 两个等级.对每种产品,两道工序的加工结果都为
两个等级.对每种产品,两道工序的加工结果都为 级时,产品为一等品,其余均为二等品。
级时,产品为一等品,其余均为二等品。
(1)已知甲、乙两种产品每一道工序的加工结果为A级的概率如表一所示,分别求生产出的甲、乙产品为一等品的概率 ;
;



(2)已知一件产品的利润如表二所示,用 分别表示一件甲、乙产品的利润,在(1)的条件下,求
分别表示一件甲、乙产品的利润,在(1)的条件下,求 的分布列及
的分布列及 ;
;
(3)已知生产一件产品需用的工人数和资金额如表三所示。该工厂有工人 名,可用资金
名,可用资金
 万元。设
万元。设 分别表示生产甲、乙产品的数量,在(2)的条件下,
分别表示生产甲、乙产品的数量,在(2)的条件下, 为何值时,
为何值时, 最大?最大值是多少?(解答时须给出图示说明)
最大?最大值是多少?(解答时须给出图示说明)
查看答案和解析>>
科目:高中数学 来源:2013届四川省成都外国语学校高二下学期期中考试数学试卷(解析版) 题型:解答题
(本小题满分12分)为了了解某工厂开展群众体育活动的情况,拟采用分层抽样的方法从A,B,C三个区中抽取7个工厂进行调查,已知A,B,C区中分别有18,27,18个工厂
(Ⅰ)求从A,B,C区中分别抽取的工厂个数;
(Ⅱ)若从抽取的7个工厂中随机抽取2个进行调查结果的对比,求这2个工厂中至少有1个来自A区的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分12分)
在“环境保护低碳生活知识竞赛”第一环节测试中,设有A、B、C三道必答题,分值依次为20分、30分、50分.竞赛规定:若参赛选手连续两道题答题错误,则必答题总分记为零分;否则各题得分之和记为必答题总分已知某选手回答A、B、C三道题正确的概率分别为![]() 、
、![]() 、
、![]() ,且回答各题时相互之间没有影响
,且回答各题时相互之间没有影响
(I) 若此选手按A、B、C的顺序答题,求其必答题总分为70分的概率;
(Ⅱ).若此选手可以自由选择答题顺序,求其必答题总分为50分的概率;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com