
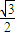 ,顶角的正弦值是底角正弦值的
,顶角的正弦值是底角正弦值的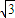 倍,则该三角形一腰的长为( )
倍,则该三角形一腰的长为( )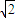
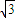
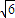
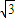 倍列出关系式,利用诱导公式及二倍角的正弦函数公式化简,得到顶角一半的正弦值,利用特殊角的三角函数值求出顶角的度数,又设腰长为m,根据三角形的面积公式表示出三角形的面积S,让面积等于
倍列出关系式,利用诱导公式及二倍角的正弦函数公式化简,得到顶角一半的正弦值,利用特殊角的三角函数值求出顶角的度数,又设腰长为m,根据三角形的面积公式表示出三角形的面积S,让面积等于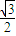 列出关于m的方程,求出方程的解即可得到m的值即为三角形的腰长.
列出关于m的方程,求出方程的解即可得到m的值即为三角形的腰长.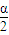 ,腰长为m,m>0,
,腰长为m,m>0,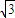 sin(90°-
sin(90°-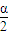 )=
)=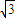 cos
cos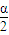 ,即2sin
,即2sin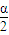 cos
cos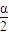 =
=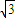 cos
cos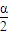 ,
,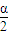 =
=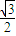 ,
,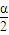 =60°,所以α=120°,
=60°,所以α=120°, m2sinα=
m2sinα=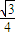 m2=
m2=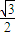 ,即m2=2,m>0,
,即m2=2,m>0,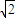 .
.

科目:高中数学 来源:2011年四川省绵阳市高考数学二模试卷(文科)(解析版) 题型:选择题
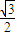 ,顶角的正弦值是底角正弦值的
,顶角的正弦值是底角正弦值的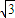 倍,则该三角形一腰的长为( )
倍,则该三角形一腰的长为( )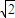

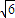
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com