
已知数列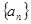 、
、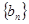 满足
满足 ,且
,且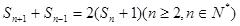 ,其中
,其中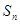 为数列
为数列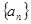 的前
的前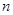 项和,又
项和,又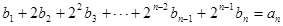 ,对任意
,对任意 都成立。
都成立。
(1)求数列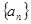 、
、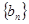 的通项公式;
的通项公式;
(2)求数列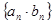 的前
的前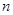 项和
项和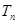
(1)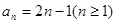 ,
,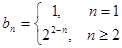 ;(2)
;(2)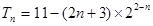 .
.
【解析】
试题分析:本题考查等差数列与等比数列的概念、通项公式、前n项和公式、数列求和等基础知识,考查运算能力和推理论证能力.第一问,将已知条件中的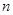 用
用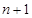 代替得到新的式子,两式子作差,得出
代替得到新的式子,两式子作差,得出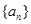 为等差数列,注意需检验
为等差数列,注意需检验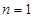 的情况,将
的情况,将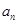 求出代入到已知的第2个式子中,用
求出代入到已知的第2个式子中,用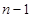 代替式子中的
代替式子中的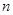 ,两式子作差得到
,两式子作差得到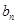 表达式;第二问,将
表达式;第二问,将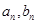 代入到
代入到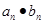 中,用错位相减法求和.
中,用错位相减法求和.
试题解析:(1)∵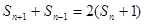 ,∴
,∴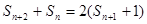
两式作差得: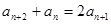
∴当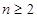 时,数列
时,数列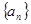 是等差数列,首项
是等差数列,首项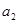 为3,公差为2,
为3,公差为2,
∴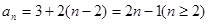 ,又
,又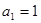 符合
符合
即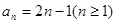 4分
4分
∵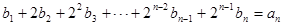 ,
,
∴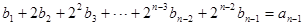
两式相减得: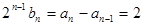 ,∴
,∴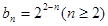
∵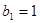 不满足,∴
不满足,∴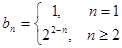 6分
6分
(2)设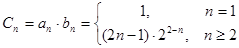
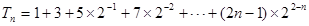
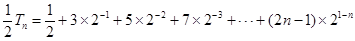
两式作差得: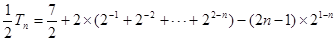
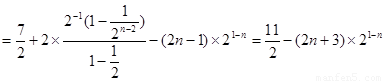
所以,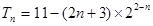 ..12分
..12分
考点:1.等差数列的通项公式;2.等比数列的前n项和;3.错位相减法求和.


 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:高中数学 来源:2011年江西省新余市高考数学二模试卷(文科)(解析版) 题型:解答题
 ,且[3+(-1)n]an+2-2an+2[(-1)n-1]=0,n∈N*.
,且[3+(-1)n]an+2-2an+2[(-1)n-1]=0,n∈N*.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com