
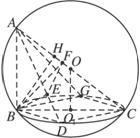
如下图,
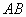 是⊙
是⊙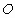 的直径,点
的直径,点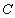 是⊙
是⊙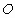 上的动点,过动点
上的动点,过动点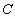 的直线
的直线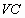 垂直于⊙
垂直于⊙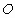 所在平面,
所在平面,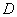 ,
,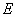 分别是
分别是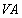 ,
,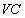 的中点.试判断直线
的中点.试判断直线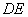 与平面
与平面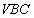 的位置关系,并说明理由.
的位置关系,并说明理由.
 优加精卷系列答案
优加精卷系列答案科目:高中数学 来源:导学大课堂必修二数学苏教版 苏教版 题型:044
如下图,AB是⊙O的直径,PA垂直于⊙O所在的平面,C为圆周上不同于A、B的一点.
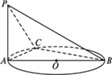
(1)当点C在圆周上运动时,问二面角A-PC-B的大小是否随之而变化?并证明你的结论.
(2)过圆心O如何作平面PBC的垂线?试研究垂足的位置,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源:广东省恩城中学2009届高三上学期模拟考试(数学理) 题型:022
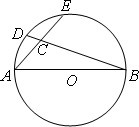
如下图,AB是⊙O的直径,D是![]() 的中点,∠ABD=20°,则∠BCE=________.(答案用数值表示)
的中点,∠ABD=20°,则∠BCE=________.(答案用数值表示)
查看答案和解析>>
科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源: 题型:
(1)求证:平面ABD⊥平面ADC;
(2)如果球半径为![]() ,D分弧BC为两部分,且弧BD∶弧DC=1∶2,求AC与BD所成的角以及AC与BD的距离.
,D分弧BC为两部分,且弧BD∶弧DC=1∶2,求AC与BD所成的角以及AC与BD的距离.
查看答案和解析>>
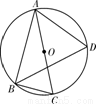
科目:高中数学 来源:2010-2011学年湖南省十二校高三第一次联考数学理卷 题型:填空题
.如下图,AC是⊙O的直径,B是圆上一点,∠ABC的平分线与⊙O相交于D,已知BC=1,AB=,则AD= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com