设向量
.
（Ⅰ）求
；
（Ⅱ）若函数
，求
的最小值、最大值.
【解析】第一问中，利用向量的坐标表示，表示出数量积公式可得
第二问中，因为，即
换元法
令
得到最值。
解：（I）
（II）由（I）得：
令
.
时，
名校课堂系列答案科目：高中数学 来源： 题型：
,
,0),点D在平面yOz上,且∠BDC=90°,∠DCB=30°.(1)求向量
的坐标;
(2)设向量
和
的夹角为θ,求cosθ的值.
查看答案和解析>>
科目：高中数学 来源：2008-2009学年重庆市渝中区求精中学高一（下）期末数学模拟试卷（1）（解析版） 题型：解答题
，
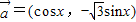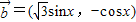，函数
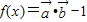，求f（x）的最大值、最小正周期和单调区间．查看答案和解析>>
科目：高中数学 来源：2010年河北省高二下学期期末考试数学（理）试题 题型：解答题
（本小题满分10分）
锐角三角形ABC的三内角A、B、C所对边的长分别为
，设向量
，且
（Ⅰ）求角B的大小；
（Ⅱ）若
，求
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
时，
，
若
，
，求
的值。
，
，函数
，求f（x）的最大值、最小正周期和单调区间．