
分析 作出不等式组对应的平面区域,利用目标函数的几何意义,进行求解即可.
解答 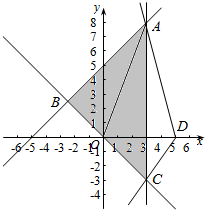 解:作出不等式组对应的平面区域,
解:作出不等式组对应的平面区域,
①μ=x2+y2的几何意义是区域内的点到原点的距离的平方,
由图象知μ=x2+y2的最小值为0,
OA的值最大,
由$\left\{\begin{array}{l}{x=3}\\{x-y+5=0}\end{array}\right.$,得$\left\{\begin{array}{l}{x=3}\\{y=8}\end{array}\right.$,即A(3,8),
此时μ=32+82=9+64=73;
②μ=$\frac{y}{x-5}$的几何意义是区域内的点到定点D(5,0)的斜率,
由图象知AD的斜率最小,此时k=$\frac{8}{3-5}=\frac{8}{-2}$=-4,
AD的斜率最大,由$\left\{\begin{array}{l}{x=3}\\{x+y=0}\end{array}\right.$得$\left\{\begin{array}{l}{x=3}\\{y=-3}\end{array}\right.$,即C(3,-3)
此时k=$\frac{-3}{3-5}=\frac{-3}{-2}$=$\frac{3}{2}$.
点评 本题主要考查线性规划的应用,利用两点间的距离公式以及直线的斜率公式是解决本题的关键.


科目:高中数学 来源: 题型:解答题
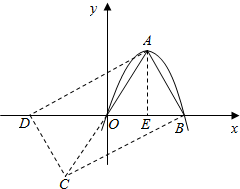 如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{ab}m$ | B. | $\frac{a+b}{2}m$ | C. | am | D. | bm |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com