袋中有4张红牌和10张黑牌,规定取出一张红牌得3分,取出一张黑牌得2分,如果从中一次取出若干张牌得26分,则不同的取牌方法共有 种(用数字表示).
【答案】
分析:分析从中一次取出若干张牌得26分的可能情况,利用组合知识,即可得到结论.
解答:解:(1)如果取出1张红牌,其余都是黑牌,但这种不可能等于26;
(2)如果取出2张红牌,其余都是黑牌,3×2+2×10=26,就是2张红牌,10张黑牌,这样有
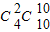
=6种;
(3)如果取出3张红牌,其余都是黑牌,这种不可能等于26;
(4)如果取出4张红牌,其余都是黑牌,3×4+2×7=26,就是4张红牌,7张黑牌,这样有
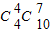
=120种
这样总共的不同的取牌方法共有120+6=126种
故答案为126.
点评:本题考查分类计数原理的运用,考查组合知识,考查学生分析解决问题的能力,属于中档题.
