例5.设f(x)=x2+px+q,A={x|x=f(x)},B={x|x=f[f(x)]},
(1)求证:A∪B=B;
(2)如果A={-1,3},求B.
【答案】
分析:(1)分析题意,要证A∪B=B,只需证明A⊆B即可,先设x∈A,根据题意,易得f[f(x)]=f(x)=x,易得x∈B,进而可得A⊆B,即可得证.
(2)根据题意,A={-1,3},即x=x
2+px+q有两根-1,3;根据根与系数的关系可得p、q的值,即可得f(x)的解析式,代入
x=f[f(x)]可得方程式,解可得B.
解答:解:(1)证明,设x∈A,
那么,根据A的定义,f(x)=x.
所以,f[f(x)]=f(x)=x.
所以x∈B.
从而A⊆B,故有A∪B=B;
(2)A={-1,3},即x=x
2+px+q有两根-1,3;
根据根与系数的关系可得,-1+3=-(p-1),则p=-1,
(-1)×3=q,则q=-3;
故f(x)=x
2-x-3,
代入x=f[f(x)]可得,[x
2-x-3]
2-(x
2-x-3)-3=x,
化简可得,x
2-x-3=-1,x
2-x-3=3,
解可得,x=3,-1,
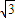
,-
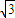
;
即B={3,-1,
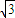
,-
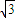
}.
点评:本题考查集合的运算,首先要认清集合的意义,如本题中两个集合是方程的解集.

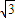 ,-
,-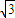 ;
;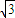 ,-
,-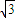 }.
}.
