
(13分)四棱锥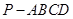 的底面是边长为1的正方形,
的底面是边长为1的正方形,
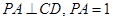 ,
,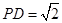 ,
,
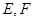 为
为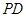 上两点,且
上两点,且
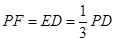 .
.
(1)求证: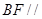 面
面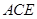 ;
;
(2)求异面直线PC与AE所成的角
(3)求二面角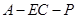 的正切值.
的正切值.

法1:(1)连BD交AC于O,连OE.
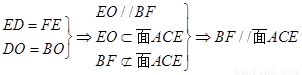
(2)过E作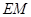
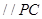 交
交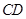 于
于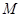 ,则
,则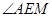 为异面直线所成的角或补角,由计算可得
为异面直线所成的角或补角,由计算可得
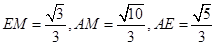 ,在
,在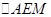 中用余弦定理可得
中用余弦定理可得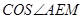
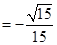 ,则异面直线所成的角为
,则异面直线所成的角为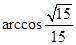 。
。
(2)由PA=1, AD=1, PD=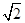
∴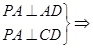 PA⊥面ACD 又CD⊥AD ∴CD⊥PD.
PA⊥面ACD 又CD⊥AD ∴CD⊥PD.
取PD中点M. ∴AM⊥面PCD, 过M作MN⊥CE交CE于N.
连AN 则∠ANM为A-EC-PE切值.
AM=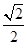 .又△MNE∽△CDE
.又△MNE∽△CDE
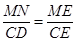 ∴
∴
Pt△AMN中, 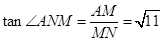
法2:以A为坐标原点.AB为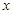 轴,AD为
轴,AD为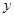 轴,AP为
轴,AP为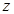 轴建立坐标系.
轴建立坐标系.
则B(1,0,0), D(0,1,0), P(0,0,1), C(1,1,0), 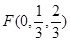 ,
E
,
E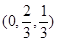
(1)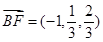 .设面ACE法向量
.设面ACE法向量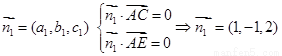
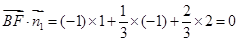
∴BF//面ACE.
(2) 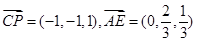 ,
,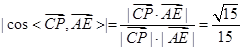 ,
,
则异面直线所成的角为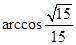
(3)设面PCE法向量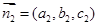 则
则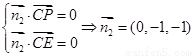
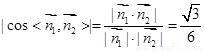
∴二面角A-EC-P的正切值为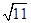 .
.
【解析】略


科目:高中数学 来源:2011-2012学年福建省泉州四校高三第二次联考考试理科数学 题型:解答题
(本小题满分13分)如图,四棱锥 的底面是正方形,
的底面是正方形, ⊥平面
⊥平面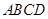 ,
,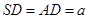 ,点E是SD上的点,且
,点E是SD上的点,且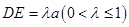 .
.
(1)求证:对任意的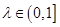 ,都有AC⊥BE;
,都有AC⊥BE;
(2)若二面角C-AE-D的大小为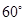 ,求
,求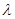 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:福建省09-10学年高二下学期期末数学理科考试试题 题型:解答题
(本小题满分13分)
如图,已知四棱锥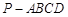 的底面是直角梯形,∠ABC
的底面是直角梯形,∠ABC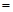 ∠BCD
∠BCD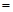 90°,AB
90°,AB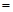 BC
BC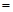 PB
PB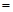 PC
PC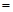 2CD
2CD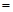 2,侧面PBC⊥底面ABCD。
2,侧面PBC⊥底面ABCD。
(1)求证: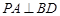 ;K^S*5U.C#O%
;K^S*5U.C#O%
(2)求二面角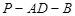 的余弦值。
的余弦值。
查看答案和解析>>
科目:高中数学 来源:2010年重庆市高三考前第一次模拟考试数学(理) 题型:解答题
(本小题满分13分 )
如题18图,已知四棱锥 的底面是边长为2的正方形,
的底面是边长为2的正方形,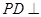 面
面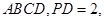
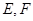 分别为
分别为 的中点.[来源:学.科.网Z.X.X.K]
的中点.[来源:学.科.网Z.X.X.K]
(Ⅰ)求直线 与面
与面 所成的角;
所成的角;
(Ⅱ)求二面角 的大小.
的大小.

查看答案和解析>>
科目:高中数学 来源:2010年重庆市高三考前第一次模拟考试数学(文) 题型:解答题
(本小题满分13分 )
已知四棱锥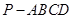 的底面是边长为2的正方形,
的底面是边长为2的正方形,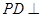
面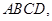
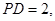
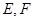 分别为
分别为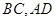 的中点,
的中点,
(Ⅰ)求直线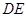 与面
与面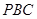 所成角的正弦值;
所成角的正弦值;
(Ⅱ)求二面角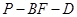 的正切值.
的正切值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com