
分析 先利用对数的真数大于0求该函数的定义域,根据函数图象来求其值域;根据题意列出不等式,通过解不等式求f(x)>1的解集.
解答 解:依题意得:4-x2>0,
解得-2<x<2,
所以该函数的定义域为:(-2,2).
∵4-x2>0,
∴(4-x2)最大值=4,
∴在(-2,2)上,该函数的值域为:(-∞,2].
由f(x)>1得到:log2(4-x2)>1,
则4-x2>2,
解得-$\sqrt{2}$<x<$\sqrt{2}$.
故不等式f(x)>1的解集为 $({-\sqrt{2},\sqrt{2}})$.
故答案是:(-2,2);(-∞,2];$({-\sqrt{2},\sqrt{2}})$.
点评 本题考查了对数函数定义域的求法,考查了对数函数的值域,是基础的计算题.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:选择题

| A. | 4n+1 | B. | 4n | C. | 4n-1 | D. | 4n-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 直线 | B. | 圆 | C. | 椭圆 | D. | 双曲线 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow a$与$λ\overrightarrow a$的方向相反 | B. | $|{λ\overrightarrow a}|≥|{\overrightarrow a}|$ | ||
| C. | $\overrightarrow a$与${λ^2}\overrightarrow a$的方向相同 | D. | $|{λ\overrightarrow a}|=|λ|\overrightarrow a$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\sqrt{2}$,$\sqrt{2}$] | B. | {-$\sqrt{2}$,$\sqrt{2}$} | C. | (-$\sqrt{2}$,$\sqrt{2}$) | D. | [0,$\sqrt{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
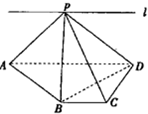 如图,ABCD为直角梯形,∠C=∠CDA=90°,AD=2BC=2CD=2,P为平面ABCD外一点,且PB⊥BD.
如图,ABCD为直角梯形,∠C=∠CDA=90°,AD=2BC=2CD=2,P为平面ABCD外一点,且PB⊥BD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com