
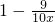 万元,当待岗员工人数x超过原有员工的5%,时,留岗员工每人每年可为企业多创利润1万元.
万元,当待岗员工人数x超过原有员工的5%,时,留岗员工每人每年可为企业多创利润1万元.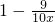 >0,x≤500×5%=25,得1≤x≤25(x∈N),
>0,x≤500×5%=25,得1≤x≤25(x∈N),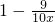 )-0.5x
)-0.5x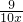 )-0.5x (1≤x≤25(x∈N))
)-0.5x (1≤x≤25(x∈N)) ,x∈N+
,x∈N+ 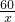 )+3500.9,
)+3500.9,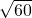 时取最小,而
时取最小,而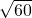 不是整数,故取x=8时y取得最大值,最大值是3384.65万元;
不是整数,故取x=8时y取得最大值,最大值是3384.65万元;

科目:高中数学 来源: 题型:
| 9 | 10x |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 9 |
| 10x |
查看答案和解析>>
科目:高中数学 来源:2011年江苏省盐城中学高考数学一模试卷(解析版) 题型:解答题
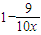 万元,当待岗员工人数x超过原有员工的5%,时,留岗员工每人每年可为企业多创利润1万元.
万元,当待岗员工人数x超过原有员工的5%,时,留岗员工每人每年可为企业多创利润1万元.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com