练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    3．设{an}是公比为q的等比数列，则“q＞1”是“{an}”为递增数列的既不充分也不必要条件（用“充分且不必要条件”，“必要且不充分条件”，“充分必要条件”，“既不充分也不必要条件”填空）

    分析 直接举反例可得答案．

    解答 解：由q＞1，数列{an}不一定是递增数列，如：-1，-2，-4，…；
    若数列{an}是递增数列，q也不一定大于1，如：-8，-4，-2，-1．
    ∴“q＞1”是“{an}”为递增数列的既不充分也不必要条件．
    故答案为：既不充分也不必要条件．

    点评 本题考查必要条件、充分条件及充要条件的判断方法，考查了数列的单调性，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    13．设f（x）=3x2ex，则f′（2）=（　　）
    A．12eB．12e2C．24eD．24e2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．已知平面内两点M（2，-2），N（4，4）．
    （Ⅰ）求MN的中垂线方程；
    （Ⅱ）求过点P（2，-3）且与直线MN平行的直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．课本介绍过平面向量数量积运算的几何意义：$\overrightarrow a•\overrightarrow b$等于$\overrightarrow a$的长度$|{\overrightarrow a}|$与$\overrightarrow b$在$\overrightarrow a$方向上的投影$|{\overrightarrow b}|cos＜\overrightarrow a，\overrightarrow b＞$的乘积．运用几何意义，有时能得到更巧妙的解题思路．例如：边长为1的正六边形ABCDEF中，点P是正六边形内的一点（含边界），则$\overrightarrow{AP}•\overrightarrow{AB}$的取值范围是$[{-\frac{1}{2}，\frac{3}{2}}]$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．若角α的终边过点P（4，-3），则cosαtanα的值为（　　）
    A．$-\frac{3}{5}$B．$\frac{4}{5}$C．$-\frac{4}{3}$D．-3

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．已知命题p：?x∈R，sinx≥-1，则￢p（　　）
    A．?x0∈R，sinx0≤-1B．?x0∈R，sinx0＜-1C．?x∈R，sinx≤-1D．?x∈R，sinx＜-1

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．袋中装有红、黄、蓝三种颜色的球各2个，无放回的从中任取3个球，则恰有两个球同色的概率为（　　）
    A．$\frac{1}{5}$B．$\frac{3}{5}$C．$\frac{2}{5}$D．$\frac{4}{5}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

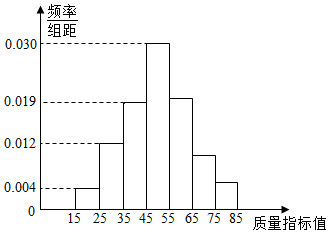    12．从某企业生产的某种产品中抽取100件，测量这些产品的质量指标值，由测量结果得到如图所示的频率分布直方图，质量指标值落在区间[55，65），[65，75），[75，85]内的频率之比为4：2：1．
    （I）求这些产品质量指标值落在区间[75，85]内的频率；
    （Ⅱ）若将频率视为概率，从该企业生产的这种产品中随机抽取3件，记这3件产品中质量指标值位于区间[45，75）内的产品件数为X，求X的分布列与数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．往边长为e的正方形OABC内任掷一点P，求P点落在阴影部分的概率．

    查看答案和解析>>

    同步练习册答案