练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】一企业从某条生产线上随机抽取30件产品，测量这些产品的某项技术指标值,得到如下的频数分布表:

    频数

    2

    6

    18

    4

    (I)估计该技术指标值的平均数和众数（以各组区间的中点值代表该组的取值）；

    (II) 若或，则该产品不合格，其余的是合格产品，从不合格的产品中随机抽取2件，求抽取的2件产品中技术指标值小于的产品恰有1件的概率．

    【答案】见解析

    【解析】(I) 该技术指标值的平均数为……3分．

    众数是……5分.

    (II)设组的4件产品分别为，组的两件产品分别为，则从不合格的产品中随机抽取2件所有基本结果为：

    ，，，，，，，，，，，，，，，共15种，……………………………………………………………………………………8分

    其中抽取的2件产品中技术指标值小于的产品恰有1件的基本结果为，，，，，，，，共8种，所以其概率为．……………………………………………………………12分

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设函数，其中，且.

    （1）求值；

    （2）若，为自然对数的底数，求证：当时，；

    （3）若函数为上的单调函数，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 ．
    （1）试判断f （x）的单调性，并证明你的结论；
    （2）若f （x）为定义域上的奇函数，求函数f （x）的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的左、右焦点分别为,设点,且=2.

    (1)求椭圆C的方程；

    (2)已知四边形MNPQ的四个顶点均在曲线C上,且MQ∥NP,MQ⊥x轴,若直线MN和直线QP交于点S(4,0)．判断四边形MNPQ两条对角线的交点是否为定点？若是,求出定点坐标；若不是,请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某厂生产某种产品x（百台），总成本为C（x）（万元），其中固定成本为2万元，每生产1百台，成本增加1万元，销售收入 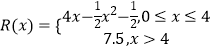（万元），假定该产品产销平衡．
    （1）若要该厂不亏本，产量x应控制在什么范围内？
    （2）该厂年产多少台时，可使利润最大？
    （3）求该厂利润最大时产品的售价．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列四个命题：（1）函数f（x）在[0，+∞）上是增函数，在（﹣∞，0）上也是增函数，所以f（x）在R上是增函数；（2）若函数f（x）=ax2+bx+2与x轴没有交点，则b2﹣8a＜0，且a＞0； （3）y=x2﹣2|x|﹣3的递增区间为[1，+∞）；（4）函数y=lg10x和函数y=elnx表示相同函数．其中正确命题的个数是（ ）
    A.3
    B.2
    C.1
    D.0

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四边形ABCD中，∠DAB=90°，∠ADC=135°，AB=5，CD=2 ，AD=2，求四边形ABCD绕AD旋转一周所成几何体的表面积及体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】给出下列四种说法： ①函数y=ax（a＞0且a≠1）与函数y=logaax（a＞0且a≠1）的定义域相同；
    ②函数y=x3与y=3x的值域相同；
    ③函数y= + 与y= 都是奇函数；
    ④函数y=（x﹣1）2与y=2x﹣1在区间[0，+∞）上都是增函数．
    其中正确的序号是（把你认为正确叙述的序号都填上）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在某城市气象部门的数据中，随机抽取了100天的空气质量指数的监测数据如表：

    空气质量指数t

    （0，50]

    （50，100]

    （100，150]

    （150，200]

    （200，300]

    质量等级

    优

    良

    轻微污染

    轻度污染

    中度污染

    严重污染

    天数K

    5

    23

    22

    25

    15

    10

    （1）在该城市各医院每天收治上呼吸道病症总人数y与当天的空气质量t（t取整数）存在如下关系y=，且当t＞300时，y＞500估计在某一医院收治此类病症人数超过200人的概率；

    （2）若在（1）中，当t＞300时，y与t的关系拟合于曲线，现已取出了10对样本数据（ti，yi）（i=1，2，3，…，10），且，求拟合曲线方程．

    （附：线性回归方程=a+bx中，b=，a=﹣b）

    查看答案和解析>>

    同步练习册答案