
(请考生在下面甲、乙两题中任选一题做答,如果多做,则按所做的甲题计分)
甲题 :
(1)若关于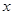 的不等式
的不等式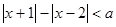 的解集不是空集,求实数
的解集不是空集,求实数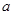 的取值范围;
的取值范围;
(2)已知实数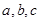 ,满足
,满足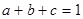 ,求
,求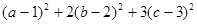 最小值.
最小值.
乙题:
已知曲线C的极坐标方程是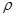 =4cos
=4cos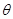 。以极点为平面直角坐标系的原点,极轴为
。以极点为平面直角坐标系的原点,极轴为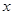 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线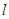 的参数方程是
的参数方程是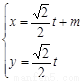 (
(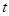 是参数)。
是参数)。
(1)将曲线C的极坐标方程化成直角坐标方程并把直线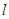 的参数方程转化为普通方程;
的参数方程转化为普通方程;
(2) 若过定点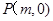 的直线
的直线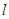 与曲线C相交于A、B两点,且
与曲线C相交于A、B两点,且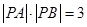 ,试求实数
,试求实数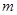 的值。
的值。
甲题:(1)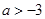
(2)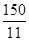
乙题:(1)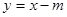
(2)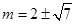 或
或
【解析】甲题:(1)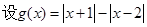 ,
,
由题意得: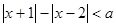 的解集不是空集,即
的解集不是空集,即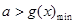 …………2分
…………2分
又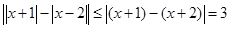 ,所以
,所以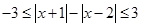
所以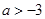 。…………7分
。…………7分
(2)由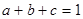 及柯西不等式得
及柯西不等式得
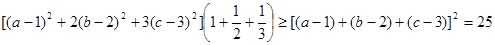 ,…11分
,…11分
所以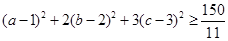 , …12分
, …12分
当且仅当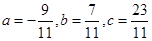 取等号,….14分
取等号,….14分
故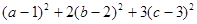 最小值为
最小值为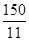 ……15分
……15分
乙题:(1)曲线C的直角坐标方程是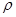 =4cos
=4cos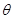 ,化为直角坐标方程为:
,化为直角坐标方程为:
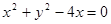 …………4分
…………4分
直线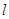 的直角坐标方程为:
的直角坐标方程为: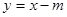 …………7分
…………7分
(2)由直线参数方程的几何意义将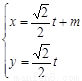
代入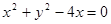 得:
得: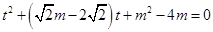 , (*)…………9分
, (*)…………9分
记两个根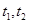 , 所以
, 所以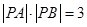 得
得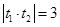 ,…………10分
,…………10分
由韦达定理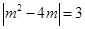 ,
,
当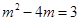 时,解得:
时,解得: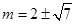 …………12分
…………12分
当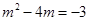 时,解得:
时,解得: …………14分
…………14分
经检验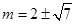 或
或 时(*)
时(*)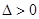 均符合题意。…………15分
均符合题意。…………15分


 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源:浙江省宁波市09-10学年高二期末八校联考数学试卷(文科) 题型:解答题
(请考生在下面甲、乙两题中任选一题做答,如果多做,则按所做的甲题计分)
甲题 :
⑴ 若关于 的不等式
的不等式 的解集不是空集,求实数
的解集不是空集,求实数 的取值范围;
的取值范围;
⑵
已知实数 ,满足
,满足 ,求
,求 最小值.
最小值.
乙题:
已知曲线C的极坐标方程是 =4cos
=4cos 。以极点为平面直角坐标系的原点,极轴为
。以极点为平面直角坐标系的原点,极轴为 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线 的参数方程是
的参数方程是 (
( 是参数)。
是参数)。
⑴ 将曲线C的极坐标方程化成直角坐标方程并把直线 的参数方程转化为普通方程;
的参数方程转化为普通方程;
⑵ 若过定点 的直线
的直线 与曲线C相交于A、B两点,且
与曲线C相交于A、B两点,且 ,试求实数
,试求实数 的值。
的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com