练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知双曲线与椭圆可
    x2
    9
    +
    y2
    25
    =1    共焦点，它们的离心率之和为
    14
    5
    ，求双曲线方程．
    分析：先根据椭圆方程求得椭圆的焦点和离心率，进而根据题意求得双曲线的焦点和离心率，进而求得双曲线方程得长轴和短轴，则双曲线方程可得．
    解答：解：依题意可知椭圆方程中a=5，b=3，
    ∴c=
    		25-9
    =4
    ∴椭圆焦点为F（O，±4），离心率为e=
    4
    5

    所以双曲线的焦点为F（O，±4），离心率为2，
    从而双曲线中
    a2+b2=16
    c
    a
    =2

    求得c=4，a=2，b=2
    		3
    ．
    所以所求双曲线方程为
    y2
    4
    -
    x2
    12
    =1
    点评：本题主要考查了双曲线的标准方程和圆锥曲线的共同特征．考查了学生对圆锥曲线的综合理解．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    给出以下5个命题：
    ①曲线x2-（y-1）2=1按
    a
    =(1，-2)    平移可得曲线（x+1）2-（y-3）2=1；
    ②设A、B为两个定点，n为常数，|
    PA
    |-|
    PB
    |=n    ，则动点P的轨迹为双曲线；
    ③若椭圆的左、右焦点分别为F1、F2，P是该椭圆上的任意一点，延长F1P到点M，使|F2P|=|PM|，则点M的轨迹是圆；
    ④A、B是平面内两定点，平面内一动点P满足向量
    AB
    与
    AP
    夹角为锐角θ，且满足 |
    PB
    | |
    AB
    | +
    PA
    •
    AB
    =0    ，则点P的轨迹是圆（除去与直线AB的交点）；
    ⑤已知正四面体A-BCD，动点P在△ABC内，且点P到平面BCD的距离与点P到点A的距离相等，则动点P的轨迹为椭圆的一部分．
    其中所有真命题的序号为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源：江西省临川十中2011－2012学年高二下学期期中考试数学理科试题 题型：022

    以下四个关于圆锥曲线的命题中：

    ①设A、B为两个定点，k为正常数，||＋||＝k，则动点P的轨迹为椭圆；

    ②双曲线与椭圆＋y2＝1有相同的焦点；

    ③方程2x2－5x＋2＝0的两根可分别作为椭圆和双曲线的离心率；

    ④已知点P(x，y)的坐标满足方程|3x＋4y－15|＝5，则点P的轨迹是一条直线．

    其中真命题的序号为________．

    查看答案和解析>>

    科目：高中数学 来源：2013届江西省高二下学期期中考试理科数学试卷（解析版） 题型：填空题

    以下四个关于圆锥曲线的命题中：

    ①设A、B为两个定点，k为正常数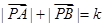，，则动点P的轨迹为椭圆；

    ②双曲线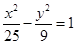与椭圆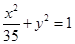有相同的焦点；

    ③方程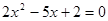的两根可分别作为椭圆和双曲线的离心率；

    ④已知点P（x,y）的坐标满足方程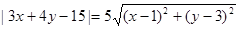，则点P的轨迹是一条直线.

    其中真命题的序号为        _______．

     

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年湖北省鄂州市高三期中考试文科数学 题型：填空题

    以下四个关于圆锥曲线的命题中：

    ①设A、B为两个定点，k为正常数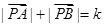，，则动点P的轨迹为椭圆；

    ②双曲线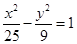与椭圆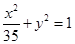有相同的焦点；

    ③方程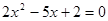的两根可分别作为椭圆和双曲线的离心率；

    ④已知点P（x,y）的坐标满足方程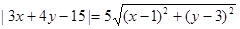，则点P的轨迹是一条直线.

    其中真命题的序号为        _______．

     

    查看答案和解析>>

    科目：高中数学 来源：2012届四川省绵阳市高二上学期期末教学质量测试数学试题 题型：填空题

    下列四个关于圆锥曲线的命题：

    ①已知M(-2，0)、N(2，0)，|PM|+|PN|=3，则动点P的轨迹是一条线段；

    ②从双曲线的一个焦点到一条渐近线的距离等于它的虚半轴长；

    ③双曲线与椭圆有共同的准线；

    ④关于x的方程x2-mx+1=0(m>2)的两根可分别作为椭圆和双曲线的离心率.

    其中正确的命题是         ．（填上你认为正确的所有命题序号）

     

    查看答案和解析>>

    同步练习册答案