练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如下图,在空间四边形ABCD中,平面ABD⊥平面BCD,且DA⊥平面ABC,则△ABC的形状为…（    ）

    A.锐角三角形            B.直角三角形           C.钝角三角形          D.不能确定

    答案：B  过A作AE⊥BD交BD于E,因为平面ABD⊥平面BCD,且∠ADB为锐角,所以DE是AD在平面BCD内的投影,又DA⊥平面ABC,所以DA⊥BC,根据三垂线定理的逆定理,可得DE⊥BC,即DB⊥BC.因为DA⊥平面ABC,所以AB是DB在平面ABC上的投影,根据三垂线定理的逆定理,可得AB⊥BC.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：湖北省荆州中学2008高考复习立体几何基础题题库二(有详细答案)人教版 人教版 题型：013

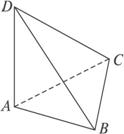
    如下图，在空间四边形ABCD中，E、F分别是AB、AD上的点，且AE∶EB＝AF∶FD＝1∶4，又H、G分别是BC、CD的中点，则

    [　　]
    A．

    BD∥平面EFGH，且EFGH是矩形

    B．

    HG∥平面ABD，且EFGH是菱形

    C．

    HE∥平面ADC，且EFGH是梯形

    D．

    EF∥平面BCD，且EFGH是梯形

    查看答案和解析>>

    科目：高中数学 来源：湖北省荆州中学2008高考复习立体几何基础题题库二(有详细答案)人教版 人教版 题型：044

    如下图，在空间四边形ABCD中，E是边AB上的一点，求作过C、E的一个平面，使对角线BD平行于这个平面，并说明理由．

    查看答案和解析>>

    科目：高中数学 来源：全优设计选修数学－2-1苏教版 苏教版 题型：044

    如下图，在空间四边形ABCD中，连结AC、BD，△BCD的重心为G，＝x＋y＋z，求x、y、z．

    查看答案和解析>>

    科目：高中数学 来源：全优设计选修数学－2-1苏教版 苏教版 题型：044

    如下图，在空间四边形OABC中，G、H分别是△ABD、△OBC的重心，设＝a，＝b，＝c．试用向量a、b、c表示向量和．

    查看答案和解析>>

    科目：高中数学 来源：全优设计选修数学－2-1苏教版 苏教版 题型：044

    如下图，在空间四边形OABC中，OA＝8，AB＝6，AC＝4，BC＝5，∠OAC＝45°，∠OAB＝60°，求OA与BC夹角的余弦值．

    查看答案和解析>>

    同步练习册答案