
已知数列 的首项为
的首项为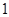 ,对任意的
,对任意的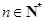 ,定义
,定义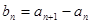 .
.
(Ⅰ)
若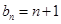 ,
,
(i)求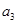 的值和数列
的值和数列 的通项公式;
的通项公式;
(ii)求数列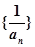 的前
的前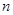 项和
项和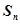 ;
;
(Ⅱ)若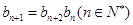 ,且
,且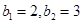 ,求数列
,求数列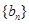 的前
的前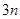 项的和.
项的和.
(1) 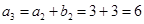 ,
, ,
,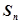
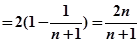
(2) 当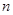 为偶数时,
为偶数时,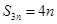 ;当
;当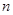 为奇数时,
为奇数时,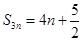
【解析】
试题分析:(Ⅰ) 解:(i)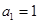 ,
, ,
,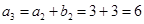 ………………2分
………………2分
由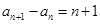 得
得
当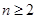 时,
时,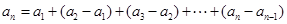
 =
=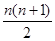 ………4分
………4分
而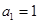 适合上式,所以
适合上式,所以 .………………5分
.………………5分
(ii)由(i)得: ……………6分
……………6分
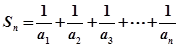
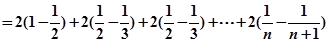 ……………7分
……………7分
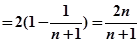 …………8分
…………8分
(Ⅱ)解:因为对任意的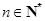 有
有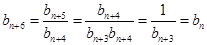 ,
,
所以数列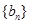 各项的值重复出现,周期为
各项的值重复出现,周期为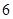 . …………9分
. …………9分
又数列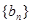 的前6项分别为
的前6项分别为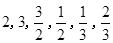 ,且这六个数的和为8. ……………10分
,且这六个数的和为8. ……………10分
设数列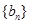 的前
的前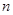 项和为
项和为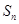 ,则,
,则,
当 时,
时,
 , ……………11分
, ……………11分
当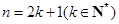 时,
时,
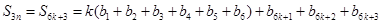
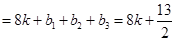 , …………12分
, …………12分
当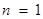 时
时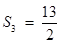
所以,当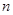 为偶数时,
为偶数时,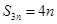 ;当
;当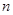 为奇数时,
为奇数时,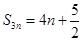 .
……………13分
.
……………13分
考点:数列的通项公式,数列的求和
点评:解决的关键是对于数列的递推关系的理解和运用,并能结合裂项法求和,以及分情况讨论求和,属于中档题。


科目:高中数学 来源: 题型:
| 5 |
| 2 |
| 3an |
| 4•2n-3n-1•an |
| 3 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年甘肃省天水市高三第三次考试文科数学试卷(解析版) 题型:解答题
(本小题12分)已知数列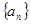 的首项为
的首项为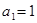 ,其前
,其前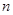 项和为
项和为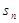 ,且对任意正整数
,且对任意正整数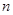 有:
有: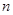 、
、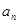 、
、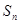 成等差数列.
成等差数列.
(1)求证:数列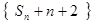 成等比数列;
成等比数列;
(2)求数列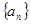 的通项公式.
的通项公式.
查看答案和解析>>
科目:高中数学 来源:河北省高三下学期第二次考试数学(文) 题型:解答题
(本小题满分12分)已知数列 的首项为
的首项为 ,前
,前 项和为
项和为 ,且对任意的
,且对任意的 ,
,
当 时,
时, 总是
总是 与
与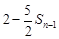 的等差中项.
的等差中项.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设 ,
, 是数列
是数列 的前
的前 项和,
项和, ,求
,求 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分14分)
已知数列![]() 的首项为
的首项为![]() ,对任意的
,对任意的![]() ,定义
,定义![]() .
.
(Ⅰ) 若![]() ,求
,求![]() ;
;
(Ⅱ) 若![]() ,且
,且![]() .
.
(ⅰ)当![]() 时,求数列
时,求数列![]() 的前
的前![]() 项和;
项和;
(ⅱ)当![]() 时,求证:数列
时,求证:数列![]() 中任意一项的值均不会在该数列中出现无数次.
中任意一项的值均不会在该数列中出现无数次.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com