
矩形ABCD(AB≤BC)中,AC=2![]() ,沿对角线AC把它折成直二面角B-AC-D后,BD=
,沿对角线AC把它折成直二面角B-AC-D后,BD=![]() ,求AB、BC的长.
,求AB、BC的长.
 |
翰林汇
AB=![]() ,BC=
,BC=![]()
如图,
 |
分别过B、D作BE⊥AC于E,DF⊥AC于F,
设∠BAC=θ,则AB=ACcosθ=2cosθ,
BE=DE=ABsinθ=sin2θ,
AE=ABcosθ=2cos2θ∴EF=AC-2AE
=2=-2cos2θ
折叠后,在平面ACD内过E作EG∥FD,且EG=FD,连接DG、BG、BD,则∠BEG为二面角B-AC-D的平面角,∴∠BEG=90°
于是BG=BE=sin2θ=2sin2θ
∴BG2+DG2=BD2,即:(2sin2θ)2+(-2cos2θ)2=5
∴4(cos2θ)2=1,∴cos2θ=±,
∵AB≤BC,∴cos2θ=-∴cosθ=,
故AB=![]() ,BC=
,BC=![]()


科目:高中数学 来源:高中数学全解题库(国标苏教版·必修4、必修5) 苏教版 题型:044
如图,设矩形ABCD(AB>AD)的周长为24,把它沿AC对折,使AB折后交DC于点P.设AB=x,求△ADP的最大面积及相应的x值.
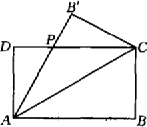
查看答案和解析>>
科目:高中数学 来源: 题型:
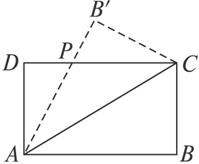
图1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com