(文)公差不为零的等差数列第2、3、6项构成等比数列,则公比为( )
A.1
B.2
C.3
D.4
【答案】
分析:等差数列的第2、3、6项依次成等比数列,所以a
32=a
2•a
6,设此等差数列的首项为a
1,公差为d,通项即为a
1+(n-1)d,得a
2=a
1+d,a
3=a
1+2d,a
6=a
1+5d,代入可得a
1和d的关系式,求出公比即可.
解答:解:设此等差数列的首项为a
1,公差为d,通项即为a
1+(n-1)d,得a
2=a
1+d,a
3=a
1+2d,a
6=a
1+5d,
又因为等差数列的第2、3、6项依次成等比数列,所以a
32=a
2•a
6,,把a
2,a
3,a
6代入可得2a
1=-d,d=-2a
1
所以公比=
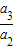
=
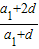
把d=-2a
1代入得公比为3.
故选C.
点评:考查学生会求等差数列通项公式的能力,会求等比数列公比的能力,以及利用等差、等比数列性质的能力.

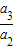 =
=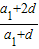 把d=-2a1代入得公比为3.
把d=-2a1代入得公比为3.
