
如图所示的几何体中,四边形ABCD是等腰梯形,AB//CD,  ,FC
,FC  平面ABCD, AE
平面ABCD, AE  BD,CB =CD=-CF.
BD,CB =CD=-CF.

(Ⅰ)求证:平面ABCD 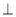 平面AED;
平面AED;
(Ⅱ)直线AF与面BDF所成角的余弦值
(Ⅰ)见解析 (Ⅱ) 
【解析】
试题分析:(Ⅰ)通过计算可证得AD⊥BD,又因为AE⊥BD,由线面垂直的判定定理得,BD⊥面ADE,由面面垂直的判定定理得,面ADE⊥面ABCD; (Ⅱ)由(Ⅰ)知AD⊥BD,同理可证AC⊥BC,因为CF⊥面ABCD,所以以CA,CB,CF分别为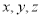 建立空间直角坐标系,设BC=1,求出A、B、D,F点的坐标,求出
建立空间直角坐标系,设BC=1,求出A、B、D,F点的坐标,求出 的坐标和平面BDF法向量的坐标,利用空间向量夹角公式计算出这两个向量夹角的余弦值,利用同脚三角函数基本关系求出向量夹角的正弦值即为线面夹角的余弦值.
的坐标和平面BDF法向量的坐标,利用空间向量夹角公式计算出这两个向量夹角的余弦值,利用同脚三角函数基本关系求出向量夹角的正弦值即为线面夹角的余弦值.
试题解析:(Ⅰ)∵四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,
∴∠ADC=∠BCD=120°,
又CB=CD,∴∠CDB=30°,∴∠ADB=90°,AD⊥BD,
又AE⊥BD,且AE∩AD=A,AE,AD?平面AED,
∴BD⊥平面AED,∴平面ABCD⊥平面AED.
(Ⅱ)连结AC,由(Ⅰ)知AD⊥BD,∴AC⊥BC,

又FC⊥平面ABCD,∴CA,CB,CF两两垂直,
以C为坐标原点,建立空间直角坐标系,设CB=1,
则A( ,0,0),B(0,1,0),D(
,0,0),B(0,1,0),D( ,
,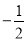 ,0),F(0,0,1),
,0),F(0,0,1),
∴ =(
=( ,
, ,0),
,0), ==(0,?1,1),
==(0,?1,1),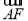 =(-
=(- ,0,1),
,0,1),
设平面BDF的一个法向量为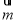 =(x,y,z),则
=(x,y,z),则 ,取z=1,则
,取z=1,则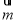 =(
=( ,1,1),
,1,1),
所以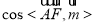 =
= ,∴直线AF与面BDF所成角的余弦值为
,∴直线AF与面BDF所成角的余弦值为 . (12分)
. (12分)
考点:空间线面垂直的判定,空间面面垂直的判定,线面角的计算,推理论证能力,运算求解能力


科目:高中数学 来源:2013-2014学年河南省长葛市毕业班第三次质量预测(三模)文科数学试卷(解析版) 题型:解答题
已知在数列{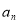 }中,
}中,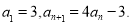
(1)求证:数列{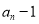 }是等比数列,并求出数列{
}是等比数列,并求出数列{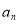 }的通项公式;
}的通项公式;
(2)设数列{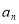 }的前竹项和为Sn,求Sn.
}的前竹项和为Sn,求Sn.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河南省毕业班高考适应性模拟练习理科数学试卷(解析版) 题型:选择题
已知三角形的三边构成等比数列,它们的公比为q,则q的一个可能的值是( )
A. B.
B. C.2 D.
C.2 D.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河南省原名校高三高考仿真模拟统一考试理科数学试卷(解析版) 题型:解答题
已知函数 
(Ⅰ)a=-3时,求不等式  的解集;
的解集;
(Ⅱ)若关于x的不等式  恒成立,求实数a的取值范围
恒成立,求实数a的取值范围
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河南省原名校高三高考仿真模拟统一考试理科数学试卷(解析版) 题型:选择题
设随机变量 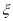 服从正态分布
服从正态分布 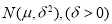 若
若 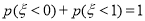 ,则
,则 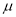 的值为
的值为
A.-1 B.l C.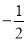 D.
D.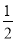
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省邯郸市高三第二次模拟考试理科数学试卷(解析版) 题型:解答题
已知函数 .
.
(1)当 时,求
时,求 在
在 处的切线方程;
处的切线方程;
(2)设函数 ,
,
(ⅰ)若函数 有且仅有一个零点时,求
有且仅有一个零点时,求 的值;
的值;
(ⅱ)在(ⅰ)的条件下,若 ,
, ,求
,求 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com