

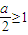
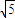 ,且△DNM∽△DAP
,且△DNM∽△DAP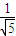 ,
,
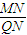 =
=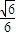


 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:高中数学 来源: 题型:
 ,已知在矩形ABCD中,AB=1,BC=a(a>0),PA⊥平面ABCD,且PA=1.
,已知在矩形ABCD中,AB=1,BC=a(a>0),PA⊥平面ABCD,且PA=1.查看答案和解析>>
科目:高中数学 来源:2014届吉林省高二4月月考理科数学试卷(解析版) 题型:解答题
如图所示,已知在矩形ABCD中,AB=1,BC=a(a>0),PA⊥平面AC,且PA=1.


(1)试建立适当的坐标系,并写出点P、B、D的坐标;
(2)问当实数a在什么范围时,BC边上能存在点Q,使得PQ⊥QD?
(3)当BC边上有且仅有一个点Q使得PQ⊥QD时,求二面角Q-PD-A的大小.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年海南省国兴中学、海师附中、嘉积中学、三亚一中高三联考数学试卷(理科)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com