
已知函数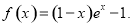
(1)求函数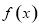 的最大值;
的最大值;
(2)若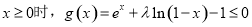 ,求
,求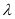 的取值范围.
的取值范围.
(3)证明: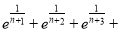 +
+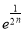
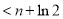 (n
(n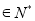 )
)
(1)0;(2) ;(3)详见解析.
;(3)详见解析.
【解析】
试题分析:(1)先求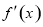 ,再利用
,再利用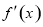 判断函数
判断函数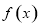 的单调性并求最值;
的单调性并求最值;
(2)思路一:由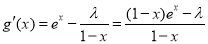 ,分
,分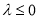 ,
,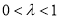 ,
, 三种情况研究函数
三种情况研究函数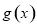 的单调性,判断
的单调性,判断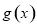 与
与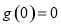 的关系,确定
的关系,确定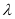 的取值范围.
的取值范围.
思路二:由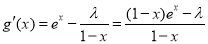 ,因为
,因为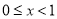 ,所以
,所以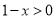
令 ,
,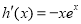 ,显然
,显然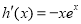
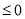 ,知
,知 为单调递减函数,
为单调递减函数,
结合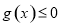 在
在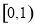 上恒成立,可知
上恒成立,可知
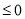 在
在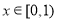 恒成立,转化为
恒成立,转化为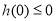 ,从而求得
,从而求得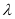 的取值范围.
的取值范围.
(3)在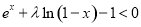 中令
中令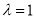 ,得
,得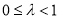 时,
时,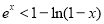 .将
.将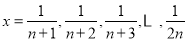 代入上述不等式,再将得到的
代入上述不等式,再将得到的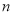 个不等式相加可得结论.
个不等式相加可得结论.
解证:(1)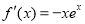 , 1分
, 1分
当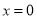 时,
时,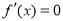 ;当
;当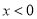 时,
时,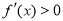 ;当
;当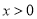 时,
时,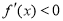 ;
;
所以函数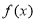 在区间
在区间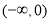 上单调递增,在区间
上单调递增,在区间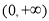 上单调递减; 3分
上单调递减; 3分
故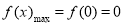 . 4分
. 4分
(2)解法一: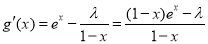 , 5分
, 5分
当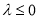 时,因为
时,因为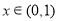 时
时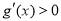 ,所以
,所以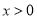 时,
时,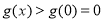 ; 6分
; 6分
当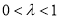 时,令
时,令 ,
,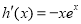 .
.
当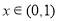 时,
时,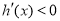 ,
,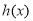 单调递减,且
单调递减,且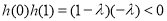 ,
,
故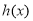 在
在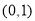 内存在唯一的零点
内存在唯一的零点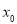 ,使得对于
,使得对于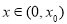 有
有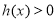 ,
,
也即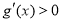 .所以,当
.所以,当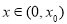 时
时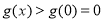 ; 8分
; 8分
当 时,
时,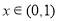 时
时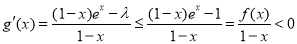 ,所以,当
,所以,当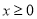 时
时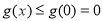 9分
9分
综上,知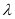 的取值范围是
的取值范围是 . 10分
. 10分
解法二: 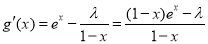 , 5分
, 5分
令 ,
,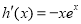 .
.
当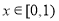 时,
时,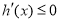 ,所以
,所以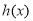 单调递减. 6分
单调递减. 6分
若在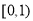 内存在使
内存在使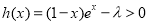 的区间
的区间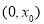 ,
,
则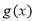 在
在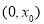 上是增函数,
上是增函数,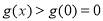 ,与已知不符. 8分
,与已知不符. 8分
故 ,
,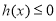 ,此时
,此时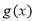 在
在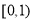 上是减函数,
上是减函数,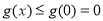 成立.
成立.
由 ,
,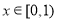 恒成立,而
恒成立,而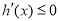 ,
,
则需 的最大值
的最大值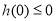 ,即
,即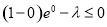 ,
, ,
,
所以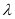 的取值范围是
的取值范围是 . 10分
. 10分
(3)在(2)中令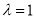 ,得
,得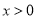 时,
时,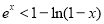 . 11分
. 11分
将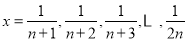 代入上述不等式,再将得到的
代入上述不等式,再将得到的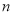 个不等式相加,得
个不等式相加,得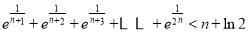 . 14分
. 14分
考点:1、导数在研究函数性质中的应用;2、函数思想解决不等式问题;3、分类讨论的思想


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:高中数学 来源:2013-2014学年山东省烟台市高三5月适应性训练一理科数学试卷(解析版) 题型:解答题
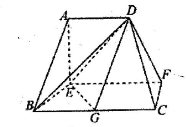
在如图所示的多面体中,底面BCFE是梯形,EF//BC,又EF 平面AEB,AE
平面AEB,AE EB,AD//EF,BC=2AD=4,EF=3,AE=BE=2,G为BC的中点.
EB,AD//EF,BC=2AD=4,EF=3,AE=BE=2,G为BC的中点.
(1)求证:AB//平面DEG;
(2)求证:BD EG;
EG;
(3)求二面角C—DF—E的正弦值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省潍坊市高三第二次模拟考试理科数学试卷(解析版) 题型:填空题
曲线 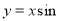 在点
在点 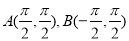 处的切线分别为
处的切线分别为 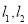 ,设
,设 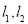 及直线 x-2y+2=0围成的区域为D(包括边界).设点P(x,y)是区域D内任意一点,则x+2y的最大值为________.
及直线 x-2y+2=0围成的区域为D(包括边界).设点P(x,y)是区域D内任意一点,则x+2y的最大值为________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省淄博市高三复习阶段性诊断考试理科数学试卷(解析版) 题型:解答题
在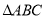 中,角A,B,C的对边分别为a,b,c,若
中,角A,B,C的对边分别为a,b,c,若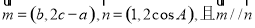 .
.
(1)求B;
(2)设函数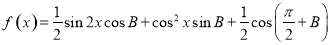 ,求函数
,求函数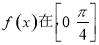 上的取值范围.
上的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省淄博市高三复习阶段性诊断考试理科数学试卷(解析版) 题型:选择题
3名男生3名女生站成两排照相,要求每排3人且3名男生不在同一排,则不同的站法有
A.324种 B.360种 C.648种 D.684种
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省济南市高三3月考模拟考试文科数学试卷(解析版) 题型:填空题
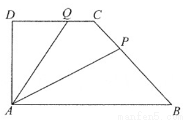
如图,在直角梯形ABCD中,AB//CD,AB=2,AD=DC=1,P是线段BC上一动点,Q是线段DC上一动点,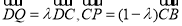 ,则
,则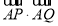 的取值范围是 .
的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com