练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    观察下列各式：则___________.
    123

    试题分析：观察可得各式的值构成数列1，3，4，7，11，…，其规律为从第三项起，每项等于其前相邻两项的和，所求值为数列中的第十项．继续写出此数列为1，3，4，7，11，18，29，47，76，123，…，第十项为123，即123，故答案为：123．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：填空题

    如图是网络工作者经常用来解释网络运作的蛇形模型：数字1出现在第1行；数字2,3出现在第2行；数字6,5,4(从左至右)出现在第3行；数字7,8,9,10出现在第4行，依此类推，则(1)按网络运作顺序第n行第1个数字(如第2行第1个数字为2，第3行第1个数字为4，…)是________；(2)第63行从左至右的第4个数字应是________．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    观察下列各式：,,，…，则的末四位数字为(    )
    A．3 125B．5 625C．0 625D．8 125

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    下列几种推理过程是演绎推理的是（　　）
    A．某校高三1班55人，2班54人，3班52人，由此得高三所有班级的人数超过50人
    B．由圆的周长C=πd推测球的表面积S=πd2
    C．两条直线平行，同旁内角互补，如果∠A与∠B是两条平行直线的同旁内角，则∠A+∠B=180°
    D．在数列{an}中，a1=1，an=（an﹣1+）（n≥2），由此归纳数列{an}的通项公式

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    要证明“”可选择的方法有以下几种，其中最合理的是     。（填序号）
    ①反证法   ②分析法    ③综合法

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    菱形的对角线相等，正方形是菱形，所以正方形的对角线相等。在以上三段论的推理中（     ）
    A．大前提错误B．小前提错误C．推理形式错误D．结论错误

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    由集合{a1}，{a1，a2}，{a1，a2，a3}，…的子集个数归纳出集合{a1，
    a2，a3，…，an}的子集个数为(  )
    A．nB．n＋1
    C．2nD．2n－1

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    在计算“1×2+2×3+...+n（n+1）”时，某同学学到了如下一种方法：
    先改写第k项：k（k+1）=
    由此得1×2=.
    .
    .............
    .
    相加，得1×2+2×3+...+n（n+1）.
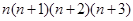    类比上述方法，请你计算“1×2×3×4+2×3×4×+....+”，其结果是_________________.（结果写出关于的一次因式的积的形式）

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    观察下列式子：，，，，……，归纳得出一般规律为               ．

    查看答案和解析>>

    同步练习册答案