
如图,在三棱锥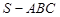 中,侧面
中,侧面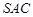 与底面
与底面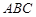 垂直,
垂直, 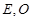 分别是
分别是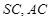 的中点,
的中点,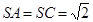 ,
,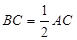 ,
,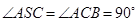 .
.
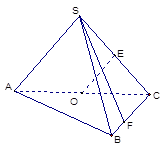
(1)若点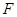 在线段
在线段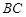 上,问:无论
上,问:无论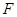 在
在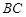 的何处,是否都有
的何处,是否都有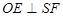 ?请证明你的结论;
?请证明你的结论;
(2)求二面角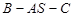 的平面角的余弦.
的平面角的余弦.
(1)详见解析;(2)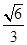
【解析】
试题分析:(1)考虑直线和直线垂直,只需考虑直线和平面垂直即可,由已知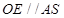 ,故可将
,故可将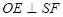 转移到判断
转移到判断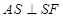 ,只需考虑
,只需考虑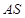 是否垂直于面
是否垂直于面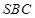 ,由已知得
,由已知得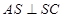 ,故只需说明
,故只需说明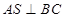 ,进而只需说明
,进而只需说明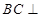 面
面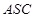 ,由已知侧面
,由已知侧面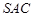 与底面
与底面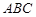 垂直,且
垂直,且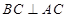 ,易证;(2)先将二面角
,易证;(2)先将二面角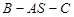 的平面角找到,再求,由(1)得
的平面角找到,再求,由(1)得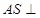 面
面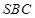 ,则
,则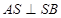 ,
,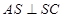 ,故
,故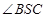 是所求的角,在
是所求的角,在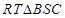 求解即可.
求解即可.
试题解析:(1)在△SAB中,∵OE∥AS,∠ASC=90°∴OE⊥SC
∵平面SAC⊥平面ABC,∠BCA=90°,∴BC⊥平面ASC,OE⊂平面ASC,
∴BC⊥OE∴OE⊥平面BSC,∵SF⊂平面BSC
∴OE⊥SF所以无论F在BC的何处,都有OE⊥SF
(2)由(1)BC⊥平面ASC∴BC⊥AS,又∵∠ASC=90°∴AS⊥SC
∴AS⊥平面BCS,∴AS⊥SB,∴∠BSC是二面角B-AS-C的平面角
在Rt△BCS中,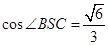
 ,所以二面角B-AS-C的平面角的余弦值为
,所以二面角B-AS-C的平面角的余弦值为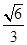 …
…
考点:1、直线和平面垂直的判定和性质;2、面面垂直的性质;3、二面角.


科目:高中数学 来源:2013-2014学年广东省中山市实验高中高三11月阶段考试文科数学试卷(解析版) 题型:解答题
如图,在三棱锥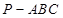 中,
中,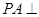 平面
平面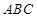 ,
,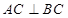 ,
,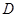 为侧棱
为侧棱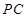 上一点,它的正(主)视图和侧(左)视图如图所示.
上一点,它的正(主)视图和侧(左)视图如图所示.
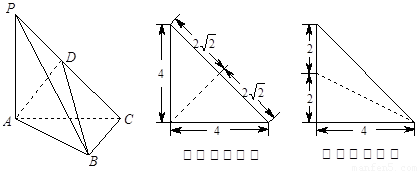
(1)证明: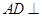 平面
平面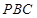 ;
;
(2)在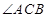 的平分线上确定一点
的平分线上确定一点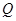 ,使得
,使得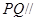 平面
平面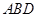 ,并求此时
,并求此时 的长.
的长.
查看答案和解析>>
科目:高中数学 来源:2014届江苏省高三开学检测理科数学试卷(解析版) 题型:解答题
如图,在四棱锥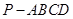 中,侧棱
中,侧棱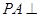 底面
底面 ,底面
,底面 为矩形,
为矩形,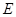 为
为 上一点,
上一点,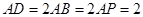 ,
,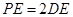 .
.
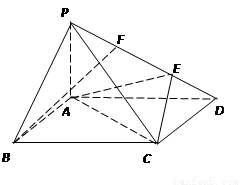
(I)若 为
为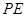 的中点,求证
的中点,求证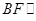 平面
平面 ;
;
(II)求三棱锥 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源:2014届江苏省高三开学检测文科数学试卷(解析版) 题型:解答题
如图,在四棱锥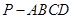 中,侧棱
中,侧棱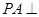 底面
底面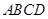 ,底面
,底面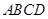 为矩形,
为矩形,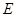 为
为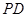 上一点,
上一点,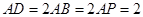 ,
,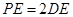 .
.
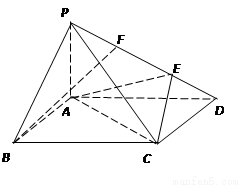
(I)若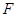 为
为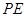 的中点,求证
的中点,求证 平面
平面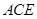 ;
;
(II)求三棱锥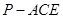 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年陕西省高三第六次适应性训练文科数学(解析版) 题型:解答题
如图,在三棱锥 中,
中, 平面
平面 ,
, ,
, 为侧棱
为侧棱 上一点,它的正(主)视图和侧(左)视图如图所示.
上一点,它的正(主)视图和侧(左)视图如图所示.
(1)证明: 平面
平面 ;
;
(2)求三棱锥 的体积;
的体积;
(3)在 的平分线上确定一点
的平分线上确定一点 ,使得
,使得 平面
平面 ,并求此时
,并求此时 的长.
的长.

查看答案和解析>>
科目:高中数学 来源:2010-2011学年北京市朝阳区高三上学期期末理科数学卷 题型:解答题
如图,在三棱锥 中,
中, ,
, ,侧面
,侧面 为等边三角形,侧棱
为等边三角形,侧棱 .
.

(Ⅰ)求证: ;
;
(Ⅱ)求证:平面 平面
平面 ;
;
(Ⅲ)求二面角 的余弦值
的余弦值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com