求经过7x+8y=38及3x-2y=0的交点且在两坐标轴上截得的截距相等的直线方程.
【答案】
分析:要求经过7x+8y=38及3x-2y=0的交点的直线方程,我们可以用直线系方程来处理,即设所求直线为7x+8y-38+λ(3x-2y)=0,然后由直线在两坐标轴上截得的截距相等构造关于λ的方程,解方程求出λ,代入即可求出满足条件的直线方程.但要注意该直线系方程不能表示直线3x-2y=0,故最后要判断一下3x-2y=0是否符合要求.
解答:解:易得交点坐标为(2,3)
设所求直线为7x+8y-38+λ(3x-2y)=0,
即(7+3λ)x+(8-2λ)y-38=0,
令x=0,y=
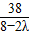
,
令y=0,x=
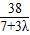
,
由已知,
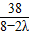
=
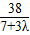
,
∴λ=

,即所求直线方程为x+y-5=0.
又直线方程不含直线3x-2y=0,
而当直线过原点时,
在两轴上的截距也相等,
故3x-2y=0亦为所求.
点评:如果两条直线的方程为:L
1、A
1x+B
1y+C
1=0及L
2、A
2x+B
2y+C
2=0,则经过两条直线交点的直线系方程为:A
1x+B
1y+C
1+λ(A
2x+B
2y+C
2)=0,但该直线系方程中不包含L
2、A
2x+B
2y+C
2=0在内.

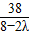 ,
,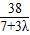 ,
,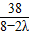 =
=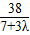 ,
, ,即所求直线方程为x+y-5=0.
,即所求直线方程为x+y-5=0.
