
分析 根据不等式的关系转化为两个函数的大小关系,构造函数g(x)=kx,h(x)=-(3x+1)ex+1,由题意得g(x)≤h(x)的整数解只有1个,求出h′(x)、判断出h(x)的单调性画出图象,利用图象和条件列出不等式组,求出实数k的取值范围.
解答 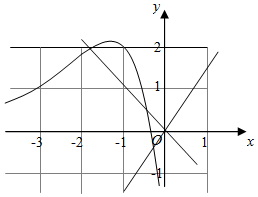 解:由f(x)≤0得(3x+1)ex+1+kx≤0,
解:由f(x)≤0得(3x+1)ex+1+kx≤0,
即kx≤-(3x+1)ex+1,
设g(x)=kx,h(x)=-(3x+1)ex+1,
h′(x)=-(3ex+1+(3x+1)ex+1)=-(3x+4)ex+1,
由h′(x)>0得:-(3x+4)>0,即x<-$\frac{4}{3}$,
由h′(x)<0得:-(3x+4)<0,即x>-$\frac{4}{3}$,
即当x=-$\frac{4}{3}$时,函数h(x)取得极大值,
由题意知,存在唯一整数m,使f(m)≤0即g(m)≤h(m),
当k≥0时,满足g(x)≤h(x)的整数解超过1个,不满足条件.
当-2≤k<0时,要使g(x)≤h(x)的整数解只有1个,
则$\left\{\begin{array}{l}{h(-1)≥g(-1)}\\{h(-2)<g(-2)}\end{array}\right.$,即$\left\{\begin{array}{l}{2•{e}^{0}≥-k}\\{5•{e}^{-1}<-2k}\end{array}\right.$,解得$-2≤k<-\frac{5}{2e}$,
所以实数k的取值范围是$[-2,-\frac{5}{2e})$,
故答案为:$[-2,-\frac{5}{2e})$.
点评 本题考查函数与不等式的应用,导数与函数单调性、极值的关系,以及构造函数法,利用构造函数和数形结合解决不等式问题,考查分析、解决问题的能力.


科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | l | D. | -4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 性别 休闲方式 | 看电视 | 运动 | 总计 |
| 女性 | 10 | 10 | 20 |
| 男性 | 10 | 50 | 60 |
| 总计 | 20 | 60 | 80 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
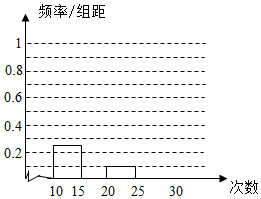 对某校高一学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数,根据数据作出了频数与频率的统计表和频率分布直方图.
对某校高一学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数,根据数据作出了频数与频率的统计表和频率分布直方图.| 分组 | 频数 | 频率 |
| [10,15) | 10 | 0.25 |
| [15,20) | 24 | n |
| [20,25) | 4 | 0.10 |
| [25,30) | m | p |
| 合计 | M | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
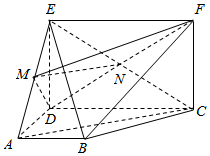 如图,矩形CDEF和梯形ABCD互相垂直,∠BAD=∠ADC=90°,AB=AD=$\frac{1}{2}$CD,BE⊥DF.
如图,矩形CDEF和梯形ABCD互相垂直,∠BAD=∠ADC=90°,AB=AD=$\frac{1}{2}$CD,BE⊥DF.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各面中,面积最小的是( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各面中,面积最小的是( )| A. | 4 | B. | 8 | C. | 4$\sqrt{5}$ | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com