已知圆C1:(x-3)2+(y+4)2=4,圆C2:x2+y2-9=0,则圆C1和圆C2的位置关系是( )
A.外离
B.外切
C.相交
D.内切
【答案】
分析:把圆C
2的方程化为标准方程,分别找出两圆的圆心坐标和半径R与r,利用两点间的距离公式求出两圆心的距离d,由d=R+r得到两圆的位置关系为外切.
解答:解:由圆C
1:(x-3)
2+(y+4)
2=4,圆C
2:x
2+y
2=9,
得到圆心C
1(3,-4),圆心C
2(0,0),且R=3,r=2,
∴两圆心间的距离d=
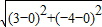
=5,
∵5=3+2,即d=R+r,
∴圆C
1和圆C
2的位置关系是外切.
故选B.
点评:此题考查了圆与圆的位置关系及其判定,以及两点间的距离公式.圆与圆位置关系的判定方法为:0≤d<R-r,两圆内含;d=R-r,两圆内切;R-r<d<R+r时,两圆相交;d=R+r时,两圆外切;d>R+r时,两圆相离(d为两圆心间的距离,R和r分别为两圆的半径).

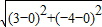 =5,
=5,

 阅读快车系列答案
阅读快车系列答案