②③
分析:①利用|AB|的最小值为抛物线的通径2p,进行判断.
②先将双曲线方程化成标准形式,再利用其几何性质求出离心率即可进行判断.
③求出两个圆的圆心和半径,再求出圆心距,由两圆的圆心距等于

,大于两圆的半径之差,小于两圆的半径之和,故两圆相交,从而得出结论.
④由直线垂直的等价条件求出两直线垂直时a的值,再判断其是否成立.
解答:①∵过抛物线y=2x
2的焦点,且与这条抛物线交于A,B两点,则|AB|的最小值为抛物线的通径2p,由抛物线y=2x
2的方程即x
2=

y 知,p=

,2p=

,则|AB|的最小值为

,故①不正确.
②双曲线
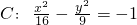
即
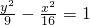
,
a=3,b=4,c=5,∴它的离心率为

;正确.
③∵⊙C
1:x
2+y
2+2x=0,即 (x+1)
2+y
2=1,表示圆心为(-1,0),半径等于1的圆.
⊙C
2:x
2+y
2+2y-1=0 即,x
2+(y+1)
2=2,表示圆心为(0,-1),半径等于

的圆.
两圆的圆心距等于

,大于两圆的半径之差,小于两圆的半径之和,故两圆相交,故两圆的公切线
由2条,故③正确.
④当直线a
2x-y+6=0与4x-(a-3)y+9=0互相垂直时,则有4a
2+(a-3)=0,解得a=-1或

,故错.
故答案为:②③.
点评:本题考查直线、抛物线、双曲线、圆的性质,两圆的位置关系,掌握圆锥曲线的性质是解题的关键.

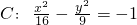 的离心率为
的离心率为 ;
; ,则这两圆恰有2条公切线;
,则这两圆恰有2条公切线; ,大于两圆的半径之差,小于两圆的半径之和,故两圆相交,从而得出结论.
,大于两圆的半径之差,小于两圆的半径之和,故两圆相交,从而得出结论. y 知,p=
y 知,p= ,2p=
,2p= ,则|AB|的最小值为
,则|AB|的最小值为  ,故①不正确.
,故①不正确.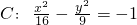 即
即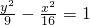 ,
, ;正确.
;正确. 的圆.
的圆. ,大于两圆的半径之差,小于两圆的半径之和,故两圆相交,故两圆的公切线
,大于两圆的半径之差,小于两圆的半径之和,故两圆相交,故两圆的公切线 ,故错.
,故错.

 阅读快车系列答案
阅读快车系列答案