
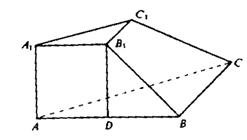
 如图,在三棱台A1B1C1-ABC中,已知A1A⊥底面ABC,A1A= A1B1= B1C1=a,B1B⊥BC,且B1B和底面ABC所成的角45??,求这个棱台的体积.
如图,在三棱台A1B1C1-ABC中,已知A1A⊥底面ABC,A1A= A1B1= B1C1=a,B1B⊥BC,且B1B和底面ABC所成的角45??,求这个棱台的体积.
![]() .
.
解:因为A1A⊥底面ABC,所以根据平面的垂线的定义有A1A⊥BC.又BC⊥BB1,且棱AA1和BB1的延长线交于一点,所以利用直线和平面垂直的判定定理可以推出BC⊥侧面A1ABB1,从而根据平面的垂线的定义又可得出BC⊥AB.
∴ △ABC是直角三角形,∠ABC=90??.并且∠ABB1就是BB1和底面ABC所成的角,
∠ABB1=45??. ——3分
作B1D⊥AB交AB于D,则B1D∥A1A,故B1D⊥底面ABC.
 ∵ Rt△B1DB中∠DBB1=45??,
∵ Rt△B1DB中∠DBB1=45??,
∴ DB=DB1=AA1=a,
∴AB=2a. ——6分
由于棱台的两个底面相似,故
Rt△ABC∽Rt△A1B1C1.
∵ B1C1=A1B1=a,AB=2a,
∴ BC=2a.
∴ S上=![]() A1B1×B1C1=
A1B1×B1C1=![]() .
.
S下=![]() AB×BC=2a2. ——8分
AB×BC=2a2. ——8分
V棱台=![]() ·A1A·
·A1A·![]()
=![]() ·a·
·a·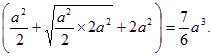 ——10分
——10分


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源:2004全国各省市高考模拟试题汇编(天利38套)·数学 题型:044
如图,在正四棱柱ABCD-A1B1C1D1中,AA1= AB,点E,M分别为A1B,C1C的中点,过点A1,B,M三点的平面A1BMN交C1D1于点N
AB,点E,M分别为A1B,C1C的中点,过点A1,B,M三点的平面A1BMN交C1D1于点N

(Ⅰ)求证:EM∥平面A1B1C1D1;
(Ⅱ)求二面角B-A1N-B1的正切值;
(Ⅲ)(文)设A1A=1,求棱台MNC1-BA1B1的体积V.
(理)设截面A1BMN把该正四棱柱截成的两个几何体的体积分别为V1,V2(V1<V2),求V1∶V2的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com