A
分析:根据题意,设数列前三项,“a
1,a
2,a
3”,数列{a
n}是递增数列,则一定有a
1<a
2<a
3,可以根据等比数列的性质、等比数列前n项和公式和根据充分必要条件的定义进行一一判断,从而求解;
解答:A、∵{a
n}是等比数列,
则由“a
1<a
2<a
3”可得数列{a
n}是递增数列,故充分性成立.
若数列{a
n}是递增数列,则一定有a
1<a
2<a
3,故必要性成立.
综上,“a
1<a
2<a
3”是“数列{a
n}是递增数列”的充分必要条件,
故A正确;
B、若“a
1<a
3<a
5”
则q
2>1,q>1或q<-1,若q>1此时“数列{a
n}是递增数列”成立,若q<-1时,数列{a
n}不是递增数列,故B错误;
C、数列{a
n}的前n项和为S
n,故 S
n =a
1+a
2+a
3+…+a
n,
若数列{a
n}是递增数列,则数列{S
n}不一定是递增数列,如当a
n<0 时,数列{S
n}是递减数列;
由数列{S
n}是递增数列,不能推出数列{a
n}的各项均为正数,如数列:0,1,2,3,…,
满足{S
n}是递增数列,但不满足等比数列{a
n},故C错误;
D、若等比数列首项为正数,且公比大于1,可以推出等比数列{a
n}为递增数列;
若等比数列{a
n}为递增数列,可以取a
1<0,0<q<1,∴a
n<0,

=
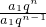
=q<1,∴a
n<a
n+1,则满足{a
n}是递增数列,
不需要首项为正数,公比q大于1,故D错误;
故选A;
点评:本题考查充分条件、必要条件的定义,递增数列的定义,判断充分性是解题的难点,此题是一道综合题,属于基础题.

 =
=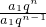 =q<1,∴an<an+1,则满足{an}是递增数列,
=q<1,∴an<an+1,则满足{an}是递增数列,

 名校课堂系列答案
名校课堂系列答案