
用0,1,2,3,4,5六个数字:
(1)能组成多少个没有重复数字的四位数;
(2)能组成多少个没有重复数字的四位偶数;
(3)能组成多少个能被5整除的没有重复数字的四位数;
(4)能组成多少个没有重复数字的比3210大的四位数。
(1)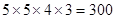
(2)个位是0: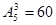 ;个位是2或4:
;个位是2或4: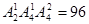 所以共60+96=156个
所以共60+96=156个
(3)个位是0: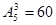 ;个位是5:
;个位是5: 所以共60+48=108个
所以共60+48=108个
(4)共有148个。
【解析】本试题主要是考查了运用排列数公式和分步计数原理求解排数问题的运用。
(1)因为要注意首位不能为零,先确定首位的数字,然后其余的数字任意选择即可。并排列。
(2)因为是偶数,既要满足末尾是偶数,同时首位不能为零,特殊位置优先考虑。
(3)因为是能被5整除的没有重复数字的四位数,只要末尾是0或者5两种情况分类讨论可知。
(4)因为没有重复数字的比3210大的四位数,因此要考虑首位比3大的情况,然后就是首位相同,十位上数字比2大,依次类推分类讨论得到。
(1)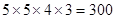
(2)个位是0: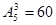 ;个位是2或4:
;个位是2或4: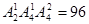 所以共60+96=156个
所以共60+96=156个
(3)个位是0: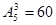 ;个位是5:
;个位是5: 所以共60+48=108个
所以共60+48=108个
(4)共有148个。


科目:高中数学 来源: 题型:
A.48 B
查看答案和解析>>
科目:高中数学 来源: 题型:
用0,1,2,3,4,5组成无重复数字的五位数,其中
(1)偶数有多少个?
(2)个位数字大于十位数字的有多少个?
(3)大于31 250的数字共有多少个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com