Question

在二项式（x²+1）⁵的展开式中含x⁴项的系数是    （用数字作答）．

Answer 1

【答案】分析：根据所给的二项式，利用二项展开式的通项公式写出第r+1项，整理成最简形式，令x的指数为4求得r，再代入系数求出结果．
解答：解：根据所给的二项式写出展开式的通项，
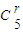
T_r+1=（x²）^5-r=x^10-2r；
要求x⁴的项的系数
∴10-2r=4，
∴r=3，
∴x⁴的项的系数是C₅³=10
故答案为：10．
点评：本题考查二项式定理的应用，本题解题的关键是正确写出二项展开式的通项，在这种题目中通项是解决二项展开式的特定项问题的工具．