Question

14．设不等式组$\left\{\begin{array}{l}{x-y+1≥0}\\{2x-y-2≤0}\\{x≥0}\\{y≥0}\end{array}\right.$表示的平面区域的面积为a，则（$\sqrt{x}$-$\frac{2a}{7x}$）²⁰¹⁵的展开式中系数最小的项是第1007项．（用数字作答）

Answer 1

分析 作出平面区域，由线性规划的知识可得a值，可得二项展开式，由组合数的知识可得．

解答 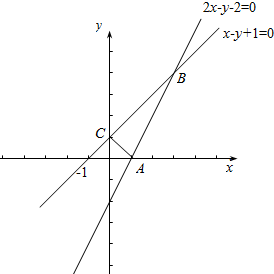解：作出不等式组$\left\{\begin{array}{l}{x-y+1≥0}\\{2x-y-2≤0}\\{x≥0}\\{y≥0}\end{array}\right.$表示的平面区域（四边形OABC），
易得OA=OC=1，S_△OAC=$\frac{1}{2}×1×1$=$\frac{1}{2}$，
联立$\left\{\begin{array}{l}{x-y+1=0}\\{2x-y-2=0}\end{array}\right.$可解得B（3，4），
B到直线AC：x+y-1=0距离d=$\frac{6}{\sqrt{{1}^{2}+{1}^{2}}}$=3$\sqrt{2}$，
∴S_△ABC=$\frac{1}{2}×\sqrt{2}×3\sqrt{2}$=3，
∴面积a=$\frac{1}{2}$+3=$\frac{7}{2}$，
∴（$\sqrt{x}$-$\frac{2a}{7x}$）²⁰¹⁵=（$\sqrt{x}$-$\frac{1}{x}$）²⁰¹⁵，
∴展开式的通项为T_k+1=${C}_{2015}^{k}$（$\sqrt{x}$）^2015-k（-$\frac{1}{x}$）^k=（-1）^k${C}_{2015}^{k}$${x}^{\frac{2015-3k}{2}}$，
∴展开式中系数为（-1）^k${C}_{2015}^{k}$，当k=1007时，系数取最小值．
故答案为：1007．

点评 本题考查简单线性规划，涉及二项式定理和作可行域，属中档题．