
设函数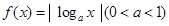 的定义域为
的定义域为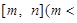
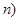 ,值域为
,值域为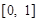 ,若
,若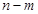 的最小值为
的最小值为 ,则实数a的值为(
)
,则实数a的值为(
)
A.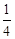 B.
B.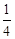 或
或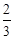 C.
C.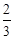 D.
D.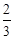 或
或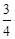
D
【解析】
试题分析:①若1≤m<n,则f(x)=-logax,
∵f(x)的值域为[0,1],∴f(m)=0,f(n)=1,解得m=1,n=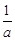 ,
,
又∵n-m的最小值为 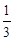 ,∴
,∴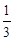 -1≥
-1≥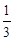 ,及0<a<1,当等号成立时,解得a=
,及0<a<1,当等号成立时,解得a=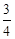 .
.
②若0<m<n<1,则f(x)=logax,
∵f(x)的值域为[0,1],∴f(m)=1,f(n)=0,解得m=a,n=1,又∵n-m的最小值为 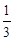 ,∴1-a≥
,∴1-a≥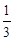 ,
,
及0<a<1,当等号成立时,解得a=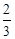 .
.
③若0<m<1<n时,不满足题意,故选D。
考点:本题主要考查对数函数的性质,绝对值的概念。
点评:中档题,注意运用分类讨论思想,确定m,n,的可能情况。本题易错,忽视不同情况的讨论。


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年东城区示范校质检一)(本小题满分14分)
设函数![]() 的定义域为全体R,当x<0时,
的定义域为全体R,当x<0时,![]() ,且对任意的实数x,y∈R,有
,且对任意的实数x,y∈R,有![]() 成立,数列
成立,数列![]() 满足
满足![]() ,且
,且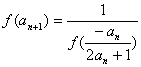 (n∈N*)
(n∈N*)
(Ⅰ)求证:![]() 是R上的减函数;
是R上的减函数;
(Ⅱ)求数列![]() 的通项公式;
的通项公式;
(Ⅲ)若不等式![]() 对一切n∈N*均成立,求k的
对一切n∈N*均成立,求k的
最大值.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年辽宁省抚顺二中高三(上)第一次月考数学试卷(理科)(解析版) 题型:解答题
 .
. 的定义域为集合B,若A⊆B,求实数a的取值范围.
的定义域为集合B,若A⊆B,求实数a的取值范围.查看答案和解析>>
科目:高中数学 来源:2011-2012学年陕西省高三第四次模拟考试理科数学试卷 题型:填空题
设函数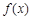 的定义域为
的定义域为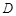 ,若存在非零实数
,若存在非零实数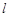 使得对于任意
使得对于任意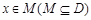 ,有
,有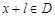 ,且
,且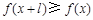 ,则称
,则称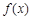 为
为 上的
上的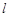 高调函数.如果定义域为
高调函数.如果定义域为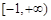 的函数
的函数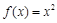 为
为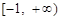 上的
上的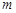 高调函数,那么实数
高调函数,那么实数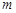 的取值范围是 .如果定义域为
的取值范围是 .如果定义域为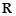 的函数
的函数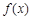 是奇函数,当
是奇函数,当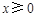 时,
时,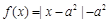 ,且
,且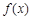 为
为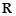 上的4高调函数,那么实数
上的4高调函数,那么实数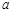 的取值范围是 .
的取值范围是 .
查看答案和解析>>
科目:高中数学 来源:2011年辽宁省瓦房店市五校高二上学期竞赛数学理卷 题型:解答题
.(本小题满分12分)设函数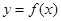 的定义域为R,当
的定义域为R,当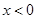 时,
时, ,且对任意实数
,且对任意实数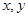 ,都有
,都有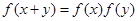 成立,数列
成立,数列 满足
满足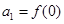 且
且
(1)求 的值;
的值;
(2)若不等式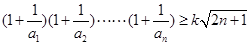 对一切
对一切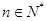 均成立,求
均成立,求 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com