
分析 (1)依题意,未租出的车辆数为$\frac{3600-3000}{50}$=12,进而可得结论;
(2)通过设每辆车的月租金为x元,配方、计算可知租赁公司的月收益y=-$\frac{1}{50}$(x-4100)2+29×104,进而可得结论.
解答 解:(1)当每辆车的月租金为3600元时,未租出的车辆数为$\frac{3600-3000}{50}$=12,
所以此时租出了100-12=88辆;
(2)设每辆车的月租金为x元,租赁公司的月收益为
y=(100-$\frac{x-3000}{50}$)(x-300)-$\frac{x-3000}{50}$×100-4200
=$\frac{1}{50}$(8000x-x2+300x-240×104+30×104-100x)-4200
=$\frac{1}{50}$(-x2+8200x-210×104)-4200
=-$\frac{1}{50}$(x-4100)2+29×104
≤29×104,
所以当每辆车的租金为4100元时,租凭公司的月收益最大,最大月收益是29万元.
点评 本题考查函数模型的选择与应用,考查分析问题、解决问题的能力,注意解题方法的积累,属于中档题.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,+∞) | B. | (1,+∞) | C. | [1,3) | D. | [1,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
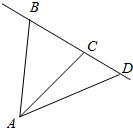 如图,设A,B,C是不共线的三点,$\overrightarrow{AB}=\overrightarrow p,\overrightarrow{AC}=\overrightarrow q$,若点D在线段BC上,且BC:CD=5:2,则向量$\overrightarrow{AD}$=$\frac{7}{5}\overrightarrow{q}-\frac{2}{5}\overrightarrow{p}$(用向量$\overrightarrow p,\overrightarrow q$表示).
如图,设A,B,C是不共线的三点,$\overrightarrow{AB}=\overrightarrow p,\overrightarrow{AC}=\overrightarrow q$,若点D在线段BC上,且BC:CD=5:2,则向量$\overrightarrow{AD}$=$\frac{7}{5}\overrightarrow{q}-\frac{2}{5}\overrightarrow{p}$(用向量$\overrightarrow p,\overrightarrow q$表示).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
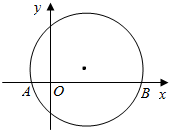 已知动圆M过点P(0,2),且在x轴上截得的弦AB的长为4.
已知动圆M过点P(0,2),且在x轴上截得的弦AB的长为4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com