
【题目】已知数列{an}的前n项和Sn满足Sn=2an-n.
(1)求数列{an}的通项公式;
(2)设![]() ,记数列{bn}的前n项和为Tn,证明:
,记数列{bn}的前n项和为Tn,证明:![]()
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
试题分析:(1)由题意得![]() ,得出
,得出![]() ,相减得到
,相减得到![]() ,进而得到数列
,进而得到数列![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列,即可求解数列的通项公式;(2)由(1)得出
的等比数列,即可求解数列的通项公式;(2)由(1)得出![]() ,转化为
,转化为![]() ,表示出
,表示出![]()
![]() ,根据放缩法即可得以证明.
,根据放缩法即可得以证明.
试题解析:(1)因为Sn=2an-n,所以当n=1时,S1=a1=2a1-1,
所以a1=1.又Sn+1=2an+1-n-1,得an+1=2an+1-2an-1,得an+1+1=2(an+1),
又a1+1=2,所以an+1=2n,故an=2n-1.
(2)证明:因为bn=![]() =
=![]() ,
,
所以bn-![]() =-
=-![]() ,所以Tn-
,所以Tn-![]() =-(
=-(![]() +
+![]() +…+
+…+![]() )<0,
)<0,
得Tn-![]() <0.又
<0.又![]() =
=![]() ≤
≤![]() ,
,
所以Tn-![]() ≥-
≥-![]() (
(![]() )=-
)=-![]() +
+![]() >-
>-![]() .所以-
.所以-![]() <Tn-
<Tn-![]() <0.
<0.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设![]() 为实数,
为实数,![]() .证明:
.证明:
(1)把![]() 写成无穷乘积有唯一的表达式
写成无穷乘积有唯一的表达式 其中,
其中,![]() 为正整数,满足
为正整数,满足![]() ;
;
(2)![]() 是有理数,当且仅当它的无穷乘积具有下列性质:存在
是有理数,当且仅当它的无穷乘积具有下列性质:存在![]() ,对所有的
,对所有的![]() ,满足
,满足![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某土特产超市为预估2020年元旦期间游客购买土特产的情况,对2019年元旦期间的90位游客购买情况进行统计,得到如下人数分布表.
购买金额(元) |
|
|
|
|
|
|
人数 | 10 | 15 | 20 | 15 | 20 | 10 |
(1)根据以上数据完成![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为购买金额是否少于60元与性别有关.
的把握认为购买金额是否少于60元与性别有关.
不少于60元 | 少于60元 | 合计 | |
男 | 40 | ||
女 | 18 | ||
合计 |
(2)为吸引游客,该超市推出一种优惠方案,购买金额不少于60元可抽奖3次,每次中奖概率为![]() (每次抽奖互不影响,且
(每次抽奖互不影响,且![]() 的值等于人数分布表中购买金额不少于60元的频率),中奖1次减5元,中奖2次减10元,中奖3次减15元.若游客甲计划购买80元的土特产,请列出实际付款数
的值等于人数分布表中购买金额不少于60元的频率),中奖1次减5元,中奖2次减10元,中奖3次减15元.若游客甲计划购买80元的土特产,请列出实际付款数![]() (元)的分布列并求其数学期望.
(元)的分布列并求其数学期望.
附:参考公式和数据: ,
,![]() .
.
附表:
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 |
| 0.150 | 0.100 | 0.050 | 0.010 | 0.005 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市的公交公司为了方便市民出行,科学规划车辆投放,在一个人员密集流动地段增设一个起点站,为了研究车辆发车间隔时间![]() 与乘客等候人数
与乘客等候人数![]() 之间的关系,经过调查得出了如下数据:
之间的关系,经过调查得出了如下数据:
间隔时间( | 10 | 11 | 12 | 13 | 14 | 15 |
等待人数( | 23 | 25 | 26 | 29 | 28 | 31 |
调查小组先从这六组数据中选取四组数据作线性回归分析,然后用剩下的两组数据进行检验
(1)求从这六组数据中选取四组数据后,剩下的的两组数据不相邻的概率:
(2)若先取的是后面四组数据,求![]() 关干
关干![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)规定根据(2)中线性回归方程预利的数据与用剩下的两组实际数据相差不超过![]() 人,则所求出的线性回归方程是“最佳回归方程”,请判断(2)中所求的是 “最佳回归方程”吗?为了使等候的乘客不超过
人,则所求出的线性回归方程是“最佳回归方程”,请判断(2)中所求的是 “最佳回归方程”吗?为了使等候的乘客不超过![]() 人,则间隔时间设置为
人,则间隔时间设置为![]() 分钟合适吗?
分钟合适吗?
附:对于一组组数据![]() , 其回归直线
, 其回归直线![]() +的斜率和截距的最小二乘估计分别为:
+的斜率和截距的最小二乘估计分别为:  ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某面包店推出一款新面包,每个面包的成本价为![]() 元,售价为
元,售价为![]() 元,该款面包当天只出一炉(一炉至少
元,该款面包当天只出一炉(一炉至少![]() 个,至多
个,至多![]() 个),当天如果没有售完,剩余的面包以每个
个),当天如果没有售完,剩余的面包以每个![]() 元的价格处理掉,为了确定这一炉面包的个数,以便利润最大化,该店记录了这款新面包最近
元的价格处理掉,为了确定这一炉面包的个数,以便利润最大化,该店记录了这款新面包最近![]() 天的日需求量(单位:个),整理得下表:
天的日需求量(单位:个),整理得下表:
日需求量 |
|
|
|
|
|
频数 |
|
|
|
|
|
(1)根据表中数据可知,频数![]() 与日需求量
与日需求量![]() (单位:个)线性相关,求
(单位:个)线性相关,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)若该店这款新面包每日出炉数设定为![]() 个
个
(i)求日需求量为![]() 个时的当日利润;
个时的当日利润;
(ii)求这![]() 天的日均利润.
天的日均利润.
相关公式: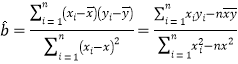 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知2件次品和3件正品混放在一起,现需要通过检测将其区分,每次随机检测一件产品,检测后不放回,直到检测出2件次品或者检测出3件正品时检测结束.
(Ⅰ)求第一次检测出的是次品且第二次检测出的是正品的概率;
(Ⅱ)已知每检测一件产品需要费用100元,设![]() 表示直到检测出2件次品或者检测出3件正品时所需要的检测费用(单位:元),求
表示直到检测出2件次品或者检测出3件正品时所需要的检测费用(单位:元),求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】每个国家对退休年龄都有不一样的规定,从2018年开始,我国关于延迟退休的话题一直在网上热议,为了了解市民对“延迟退休”的态度,现从某地市民中随机选取100人进行调查,调查情况如下表:
年龄段(单位:岁) |
|
|
|
|
|
|
被调查的人数 |
|
|
|
|
|
|
赞成的人数 |
|
|
|
|
|
|
(1)从赞成“延迟退休”的人中任选1人,此人年龄在![]() 的概率为
的概率为![]() ,求出表格中
,求出表格中![]() 的值;
的值;
(2)若从年龄在![]() 的参与调查的市民中按照是否赞成“延迟退休”进行分层抽样,从中抽取10人参与某项调查,然后再从这10人中随机抽取4人参加座谈会,记这4人中赞成“延迟退休”的人数为
的参与调查的市民中按照是否赞成“延迟退休”进行分层抽样,从中抽取10人参与某项调查,然后再从这10人中随机抽取4人参加座谈会,记这4人中赞成“延迟退休”的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着经济的发展,个人收入的提高,自2019年1月1日起,个人所得税起征点和税率的调整.调整如下:纳税人的工资、薪金所得,以每月全部收入额减除5000元后的余额为应纳税所得额.依照个人所得税税率表,调整前后的计算方法如下表:
个人所得税税率表(调整前) | 个人所得税税率表(调整后) | ||||
免征额3500元 | 免征额5000元 | ||||
级数 | 全月应纳税所得额 | 税率(%) | 级数 | 全月应纳税所得额 | 税率(%) |
1 | 不超过1500元部分 | 3 | 1 | 不超过3000元部分 | 3 |
2 | 超过1500元至4500元的部分 | 10 | 2 | 超过3000元至12000元的部分 | 10 |
3 | 超过4500元至9000元的部分 | 20 | 3 | 超过12000元至25000元的部分 | 20 |
... | ... | ... | ... | ... | ... |
(1)假如小红某月的工资、薪金等所得税前收入总和不高于8000元,记![]()
![]() 表示应纳的税,试写出调整前后
表示应纳的税,试写出调整前后![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)某税务部门在小红所在公司利用分层抽样方法抽取某月100个不同层次员工的税前收入,并制成下面的频数分布表:
收入(元) |
|
|
|
|
|
|
人数 | 30 | 40 | 10 | 8 | 7 | 5 |
先从收入在![]() 及
及![]() 的人群中按分层抽样抽取7人,再从中选2人作为新纳税法知识宣讲员,求两个宣讲员不全是同一收入人群的概率;
的人群中按分层抽样抽取7人,再从中选2人作为新纳税法知识宣讲员,求两个宣讲员不全是同一收入人群的概率;
(3)小红该月的工资、薪金等税前收入为7500元时,请你帮小红算一下调整后小红的实际收入比调整前增加了多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com