
已知如图10-21,斜三棱柱ABC-A1B1C1的侧面A1ACC1与底面ABC垂直,∠ABC=90°,BC=2,AC=2![]() ,且AA1⊥A1C,AA1=A1C.
,且AA1⊥A1C,AA1=A1C.
(Ⅰ)求侧棱A1A与底面ABC所成角的大小;
(Ⅱ)求侧面A1ABB1与底面ABC所成二面角的大小;
(Ⅲ)求顶点C到侧面A1ABB1的距离
图10-21
(Ⅰ)解:作A1D⊥AC,垂足为D,由面A1ACC1⊥面ABC,得A1D⊥面ABC
∴∠A1AD为A1A与面ABC所成的角
∵AA1⊥A1C,AA1=A1C,
∴∠A1AD=45°为所求.
(Ⅱ)解:作DE⊥AB,垂足为E,连A1E,则由A1D⊥面ABC,得A1E⊥AB,
∴∠A1ED是面A1ABB1与面ABC所成二面角的平面角.
由已知,AB⊥BC,得ED∥BC又D是AC的中点,BC=2,AC=2![]() ,
,
∴DE=1,AD=A1D=![]() ,tg∠A1ED=
,tg∠A1ED=![]() =
=![]() .
.
故∠A1ED=60°为所求.
(Ⅲ)
方法一:由点C作平面A1ABB1的垂线,垂足为H,则CH的长是C到平面A1ABB1的距离.
连结HB,由于AB⊥BC,得AB⊥HB.
又A1E⊥AB,知HB∥A1E,且BC∥ED,
∴∠HBC=∠A1ED=60°
∴CH=BCsin60°=![]() 为所求.
为所求.
方法二:连结A1B.
根据定义,点C到面A1ABB1的距离,即为三棱锥C-A1AB的高h.
由V锥C-A1AB=V锥A1-ABC得![]() S△AA1B·h=
S△AA1B·h=![]() S△ABC·A1D,
S△ABC·A1D,
即![]() ×2
×2![]() h=
h=![]() ×2
×2![]() ×3
×3
∴h=![]() 为所求.
为所求.


科目:高中数学 来源: 题型:

图1-3-10
A.2∶3 B.4∶9 C.4∶5 D.4∶21
查看答案和解析>>
科目:高中数学 来源: 题型:
(12分)评委会把同学们上交的作品的件数按5天一组分组统计,绘制了频率分布直方 图,如图所示,已知从左到右各长方形的高的比为2:3:4:6:4:1,第三组的频数为 12 ,请解答下列问题:(1)本次活动共有多少件作品参加评比?
(2)那组上交的作品量最多?有多少件?
(3)经过评比,第四组和第六组分别有10件、2件作品获奖,问这两组哪组的获奖率高?
|

查看答案和解析>>
科目:高中数学 来源: 题型:
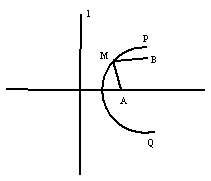
某地地震发生后,由于公路破坏严重,救灾物资需水运到合适地点再转运到受灾严重的A、B两地,如图所示,需要在两岸PQ上抢修一处码头和到A、B两地的公路。经测算,A地在损毁的公路![]() (南北向)正东方向2
(南北向)正东方向2![]() 处,B地在A地北偏东
处,B地在A地北偏东![]() 方向
方向![]()
![]() 处,河流沿岸PQ上每一点到公路
处,河流沿岸PQ上每一点到公路![]() 和A地的距离相等。已知修建公路的费用均为2万元/
和A地的距离相等。已知修建公路的费用均为2万元/![]() ,修建码头的费用是10万元,那么抢修费用最低约为
,修建码头的费用是10万元,那么抢修费用最低约为
(单位:万元)( )
A、19 B、20
C、21 D、22
查看答案和解析>>
科目:高中数学 来源: 题型:
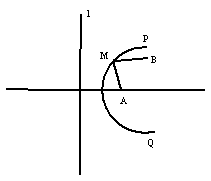
某地地震发生后,由于公路破坏严重,救灾物资需水运到合适地点再转运到受灾严重的A、B两地,如图所示,需要在两岸PQ上抢修一处码头和到A、B两地的公路。经测算,A地在损毁的公路![]() (南北向)正东方向2
(南北向)正东方向2![]() 处,B地在A地北偏东
处,B地在A地北偏东![]() 方向
方向![]()
![]() 处,河流沿岸PQ上每一点到公路
处,河流沿岸PQ上每一点到公路![]() 和A地的距离相等。已知修建公路的费用均为2万元/
和A地的距离相等。已知修建公路的费用均为2万元/![]() ,修建码头的费用是10万元,那么抢修费用最低约为
,修建码头的费用是10万元,那么抢修费用最低约为
(单位:万元)( )
A、19 B、20
C、21 D、22
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com