
已知函数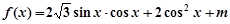 在区间
在区间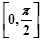 上的最大值为2.
上的最大值为2.
(1)求常数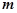 的值;
的值;
(2)在 中,角
中,角 ,
,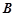 ,
,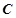 所对的边是
所对的边是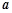 ,
,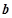 ,
, ,若
,若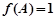 ,
, ,
, 面积为
面积为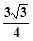 .求边长
.求边长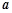 .
.
(1) (2)
(2)
【解析】本试题主要是考查了三角函数的性质和解三角形中的两个定理的运用。
(1)将已知函数化为但一三角函数,然后结合三角函数的性质得到结论。
(2)根据正弦定理和余弦定理,结合得到边的长度解:(1)
 …………………… 2分
…………………… 2分
 …………………… 4分
…………………… 4分
∵  ∴
∴ …………………… 5分
…………………… 5分
∴当 即
即 时,函数
时,函数 在区间
在区间 上取到最大值.
上取到最大值.
此时, 得
得 …………………… 7分
…………………… 7分
(2)∵  ∴
∴

∴  ,解得
,解得 (舍去)或
(舍去)或 …………………… 9分
…………………… 9分
∵  ,
,
∴  …………①
…………………… 11分
…………①
…………………… 11分
∴ 
即 …………②
…………………… 12分
…………②
…………………… 12分
由①和②解得 …………………… 13分
…………………… 13分
∵ 
∴  ……………………
14分
……………………
14分


科目:高中数学 来源:2013届陕西省高二上学期期末考试理科数学 题型:解答题
.(本小题满分12分)已知函数 在区间
在区间
 上的最大值为
上的最大值为 ,最小值为
,最小值为 .
.
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)若函数 在区间
在区间 上为减函数,求实数
上为减函数,求实数 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com