【答案】
分析:由
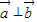
,可得
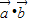
=cosθsinθ+

=0,求得sin2θ 的值; 据
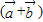
∥
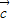
,得到 2×

=
m(sinθ+cosθ ),求出m
2的值,即可得到 m的值.
解答:解:∵
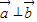
,∴
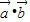
=cosθsinθ+

=0,∴sin2θ=-

.
∵
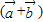
∥
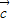
,
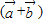
=(sinθ+cosθ,

),∴2×

=m(sinθ+cosθ ),
∴
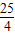
=m
2(1+sin2θ),∴m
2=
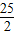
,m=±
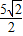
,
故答案为:±
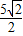
.
点评:本题考查两个向量的数量积公式的应用,两个向量垂直、平行的性质,求出 sin2θ=-

,是解题的关键.
练习册系列答案
相关习题
科目:高中数学
来源:2012-2013学年四川省高三零诊理科数学试卷(解析版)
题型:填空题
查看答案和解析>>
科目:高中数学
来源:2014届浙江省宁波四校高一下学期期中数学试卷(解析版)
题型:选择题
查看答案和解析>>
科目:高中数学
来源:2010-2011学年浙江省杭州市高三上学期第三次月考理科数学卷
题型:填空题
查看答案和解析>>
科目:高中数学
来源:2010-2011学年浙江省杭州市高三上学期第三次月考考试数学理卷
题型:填空题
查看答案和解析>>
科目:高中数学
来源:2010年江西省宜春市高一下学期第一次月考数学卷
题型:填空题
查看答案和解析>>

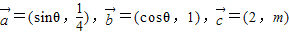 满足
满足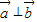 且
且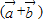 ∥
∥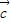 ,则实数m= .
,则实数m= .  阅读快车系列答案
阅读快车系列答案