
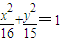 的左焦点为F,点P为椭圆上一动点,过点以F为圆心,1为半径的圆作切线PM,PN,其中切点为M,N则四边形PMFN面积的最大值 为 .
的左焦点为F,点P为椭圆上一动点,过点以F为圆心,1为半径的圆作切线PM,PN,其中切点为M,N则四边形PMFN面积的最大值 为 .  |PM|•|MF|=
|PM|•|MF|= |PM|,从而四边形PMFN面积S=2S△AFM=|PM|.根据勾股定理,得|PM|=
|PM|,从而四边形PMFN面积S=2S△AFM=|PM|.根据勾股定理,得|PM|=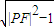 ,因此当|PF|最长时|PM|达到最大值.再根据椭圆的几何性质,得P与椭圆右顶点重合时,|PF|最长,由此可得|PM|最大值为2
,因此当|PF|最长时|PM|达到最大值.再根据椭圆的几何性质,得P与椭圆右顶点重合时,|PF|最长,由此可得|PM|最大值为2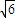 ,即得四边形PMFN面积的最大值.
,即得四边形PMFN面积的最大值.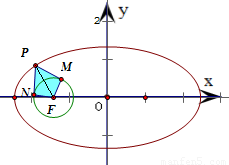 连接PF,
连接PF, |PM|•|MF|=
|PM|•|MF|= |PM|
|PM|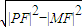 =
=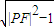
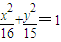 右顶点(4,0)重合时,|PF|最长.
右顶点(4,0)重合时,|PF|最长.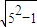 =2
=2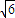


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
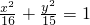 的左焦点为F,点P为椭圆上一动点,过点以F为圆心,1为半径的圆作切线PM,PN,其中切点为M,N则四边形PMFN面积的最大值 为________.
的左焦点为F,点P为椭圆上一动点,过点以F为圆心,1为半径的圆作切线PM,PN,其中切点为M,N则四边形PMFN面积的最大值 为________.查看答案和解析>>
科目:高中数学 来源:2011-2012学年湖北省宜昌一中高二(上)期中数学试卷(文科)(解析版) 题型:解答题
 的左焦点为F(-1,0),离心率为
的左焦点为F(-1,0),离心率为 ,过点F的直线l与椭圆C交于A、B两点.
,过点F的直线l与椭圆C交于A、B两点.查看答案和解析>>
科目:高中数学 来源:2011年北京市昌平区高考数学二模试卷(文科)(解析版) 题型:解答题
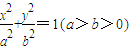 的左焦点为F(-1,0),离心率为
的左焦点为F(-1,0),离心率为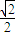 ,过点F的直线l与椭圆C交于A、B两点.
,过点F的直线l与椭圆C交于A、B两点.查看答案和解析>>
科目:高中数学 来源: 题型:
已知椭圆C1:![]() 的左焦点为F,点P为椭圆上一动点,过点P作以F为圆心,1为半径的圆的切线PM,PN,其切点为M,N,则四边形PMFN面积的最大值为____.
的左焦点为F,点P为椭圆上一动点,过点P作以F为圆心,1为半径的圆的切线PM,PN,其切点为M,N,则四边形PMFN面积的最大值为____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com