在底面直径和高均为3的圆锥内作一内接圆柱，当内接圆柱体积最大时该圆柱的侧面积为（ ）
A．π
B．2π
C．3π
D．4π
【答案】
分析：设圆柱的高为h，底面圆半径为r，然后根据题目中所提供数据求出h与r的等式关系，最后将体积表示出来，利用三元均值不等式可求出何时体积最大，再求出此时圆柱的侧面积即可．
解答：解：设圆柱的高为h，底面圆半径为r，则有2r=3-h，所以h=3-2r，
，
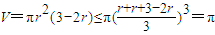
当且仅当r=3-2r即r=1=h时圆柱体积最大，此时圆柱的侧面积为2π，
故选B．
点评：本题主要考查圆柱体积公式，组合体的轴截面，三角形相似的性质；另外随解法不同，还可考查三元均值不等式或导数的应用，属于基础题．
