
如图1所示,四边形OABC是矩形,点A、C的坐标分别为(3,0),(0,1),点D是线段BC上的动点(与端点B、C不重合),过点D作直线![]() =-
=-![]() +
+![]() 交折线OAB于点E.
交折线OAB于点E.
(1)记△ODE的面积为S,求S与![]() 的函数关系式;
的函数关系式;
(2)当点E在线段OA上时,若矩形OABC关于直线DE的对称图形为四边形O1A1B1C1,试探究O1A1B1C1与矩形OABC的重叠部分的面积是否发生变化,若不变,求出该重叠部分的面积;若改变,请说明理由。

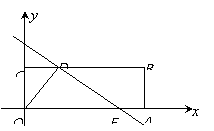

(1)由题意得B(3,1).
若直线经过点A(3,0)时,则b=![]() …………1分
…………1分
若直线经过点B(3,1)时,则b=![]() …………1分
…………1分
若直线经过点C(0,1)时,则b=1 …………1分
①若直线与折线OAB的交点在OA上时,即1<b≤![]() ,如图25-a,
,如图25-a,
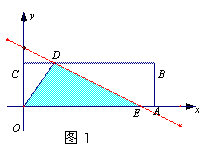

此时E(2b,0)
∴S=![]() OE·CO=
OE·CO=![]() ×2b×1=b …………2分
×2b×1=b …………2分
②若直线与折线OAB的交点在BA上时,即![]() <b<
<b<![]() ,如图2
,如图2
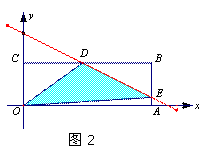

此时E(3,![]() ),D(2b-2,1)
),D(2b-2,1)
∴S=S矩-(S△OCD+S△OAE +S△DBE )
= 3-[![]() (2b-1)×1+
(2b-1)×1+![]() ×(5-2b)·(
×(5-2b)·(![]() )+
)+![]() ×3(
×3(![]() )]=
)]=![]()
…………2分
∴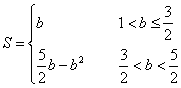 …………1分
…………1分
(2)如图3,设O1A1与CB相交于点M,OA与C1B1相交于点N,则矩形OA1B1C1与矩形OABC的重叠部分的面积即为四边形DNEM的面积。
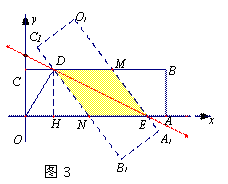

由题意知,DM∥NE,DN∥ME,∴四边形DNEM为平行四边形…………1分
根据轴对称知,∠MED=∠NED
又∠MDE=∠NED,∴∠MED=∠MDE,∴MD=ME,∴平行四边形DNEM为菱形.
…………1分
过点D作DH⊥OA,垂足为H,
由题易知,tan∠DEN=![]() ,DH=1,∴HE=2,…………1分
,DH=1,∴HE=2,…………1分
设菱形DNEM 的边长为a,
则在Rt△DHM中,由勾股定理知:![]() ,∴
,∴![]() …………1分
…………1分
∴S四边形DNEM=NE·DH=![]()
∴矩形OA1B1C1与矩形OABC的重叠部分的面积不发生变化,面积始终为![]() .
.


科目:高中数学 来源: 题型:
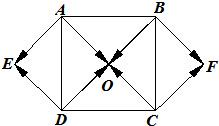 如图,O是正方形ABCD对角线的交点,四边形OAED,OCFB都是正方形,在图中所示的向量中:
如图,O是正方形ABCD对角线的交点,四边形OAED,OCFB都是正方形,在图中所示的向量中:| AO |
| AO |
| AO |
| AO |
| CO |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
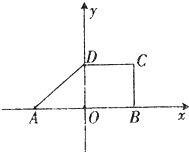 如图所示,四边形ABCD是一个梯形,CD∥AB,CD=AO=1,△AOD为等腰直角三角形,O为AB的中点,试求梯形ABCD的水平放置的直观图的面积.
如图所示,四边形ABCD是一个梯形,CD∥AB,CD=AO=1,△AOD为等腰直角三角形,O为AB的中点,试求梯形ABCD的水平放置的直观图的面积.查看答案和解析>>
科目:高中数学 来源:2012年人教A版高中数学必修四2.1平面向量的实际背景及其基本概念(解析版) 题型:解答题
如图所示,点O为正方形ABCD对角线的交点,四边形OAED,OCFB都是正方形.

在图中所示的向量中:
(1)分别写出与 ,
, 相等的向量;
相等的向量;
(2)写出与 共线的向量;
共线的向量;
(3)写出与 的模相等的向量;
的模相等的向量;
(4)向量 与
与 是否相等?
是否相等?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com