
 ,其中m∈R.
,其中m∈R. x(m2+1),由(1)得到f(x)的极大值、极小值,根据极值的符号借助图象可判断函数f(x)零点的个数;
x(m2+1),由(1)得到f(x)的极大值、极小值,根据极值的符号借助图象可判断函数f(x)零点的个数;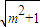 ,或x≥m+
,或x≥m+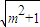 ;
;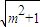 ),(m+
),(m+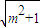 ,+∞),减区间(m-
,+∞),减区间(m-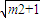 ,m+
,m+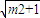 ).
).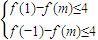 ,即
,即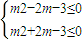 ,解得-1≤m≤1;
,解得-1≤m≤1;  x3-mx2-x+
x3-mx2-x+ m=-
m=- mx2-
mx2- x+
x+ m=-
m=- x(m2+1),
x(m2+1),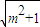 )=-
)=- (m-
(m-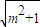 )(m2+1)>0,
)(m2+1)>0,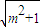 )=-
)=- (m+
(m+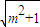 )(m2+1)<0,
)(m2+1)<0,

科目:高中数学 来源:2010-2011学年广东省广州六中高三(上)12月月考数学试卷(理科)(解析版) 题型:解答题
 ,
, 其中m∈R且m≠o.
其中m∈R且m≠o. 当m≥2时,若对于任意的x1∈[2,+∞),总存在唯一的x2∈(-∞,2),使得g(x1)=g(x2)成立.试求m的取值范围.
当m≥2时,若对于任意的x1∈[2,+∞),总存在唯一的x2∈(-∞,2),使得g(x1)=g(x2)成立.试求m的取值范围.查看答案和解析>>
科目:高中数学 来源:2011-2012学年福建师大附中高三(上)期中数学试卷(理科)(解析版) 题型:解答题
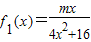 ,
,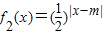 其中m∈R且m≠o.
其中m∈R且m≠o.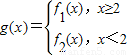 当m≥2时,若对于任意的x1∈[2,+∞),总存在唯一的x2∈(-∞,2),使得g(x1)=g(x2)成立.试求m的取值范围.
当m≥2时,若对于任意的x1∈[2,+∞),总存在唯一的x2∈(-∞,2),使得g(x1)=g(x2)成立.试求m的取值范围.查看答案和解析>>
科目:高中数学 来源:2010-2011学年福建省泉州一中高三(上)期末数学试卷(理科)(解析版) 题型:解答题
 ,
,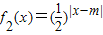 其中m∈R且m≠o.
其中m∈R且m≠o.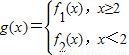 当m≥2时,若对于任意的x1∈[2,+∞),总存在唯一的x2∈(-∞,2),使得g(x1)=g(x2)成立.试求m的取值范围.
当m≥2时,若对于任意的x1∈[2,+∞),总存在唯一的x2∈(-∞,2),使得g(x1)=g(x2)成立.试求m的取值范围.查看答案和解析>>
科目:高中数学 来源:2013年高考数学压轴大题训练:函数的最值问题(解析版) 题型:解答题
 ,
, 其中m∈R且m≠o.
其中m∈R且m≠o. 当m≥2时,若对于任意的x1∈[2,+∞),总存在唯一的x2∈(-∞,2),使得g(x1)=g(x2)成立.试求m的取值范围.
当m≥2时,若对于任意的x1∈[2,+∞),总存在唯一的x2∈(-∞,2),使得g(x1)=g(x2)成立.试求m的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com