
 倍,求:(1)动点M的轨迹方程;(2)根据
倍,求:(1)动点M的轨迹方程;(2)根据 取值范围指出轨迹表示的图形.
取值范围指出轨迹表示的图形. (2)见解析
(2)见解析 倍坐标化,再化简整理即可得取点M的轨迹方程.
倍坐标化,再化简整理即可得取点M的轨迹方程.
 )
)
 ,PQ中垂线所在直线方程
,PQ中垂线所在直线方程
 ,PR中垂线所在直线方程
,PR中垂线所在直线方程
 ,圆心(4,-3),r=5圆的标准方程
,圆心(4,-3),r=5圆的标准方程


 时,直线
时,直线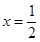
 时,
时,
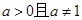 时,表示圆
时,表示圆 时,表示点(2,0)
时,表示点(2,0) 时,不表示任何图形
时,不表示任何图形

 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 的参数方程是
的参数方程是 ,圆C的极坐标方程为
,圆C的极坐标方程为 .
. 上的点向圆C引切线,求切线长的最小值.
上的点向圆C引切线,求切线长的最小值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,动点N在圆
,动点N在圆 上运动,线段MN的
上运动,线段MN的 与点P的轨迹相切,且
与点P的轨迹相切,且 在
在 轴.
轴. 轴上的截距相等,求直线
轴上的截距相等,求直线 的方程.
的方程. 查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
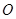 处,极轴与
处,极轴与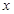 轴的正半轴重合.直线
轴的正半轴重合.直线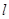 的参数方程为
的参数方程为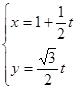 (
(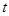 为参数),圆
为参数),圆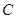 的极坐标方程为
的极坐标方程为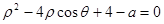 .若直线
.若直线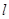 与圆
与圆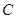 相交于
相交于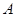 、
、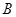 且
且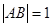 ,求实数
,求实数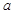 的值.
的值. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com